Das zugehörige Buch „Musik ist Leben“ kann im Verlag unter tredition.de bestellt werden.
Um die aktuellen Beiträge zu lesen bitte in der Kopfzeile nocheinmal Musik anklicken, darunter erscheint dann der Schriftzug Beiträge, der die neuesten aktuellen Nachrichten enthält.
Harmonische Musik hören oder selbst spielen ist ein Lebenselixier, ein Ohrenschmaus. Ob Pflanze, Tier oder Mensch, alle brauchen dieses Elexier um größer, stärker und weiser auf dieser Welt zu werden.
In der Schule LSH in Holzminden hörten wir in der Hohen Halle jeden Morgen zur Morgensprache von Fräulein Brigitte Bischoff, Violine, und von unserem Pianisten Hans-Joachim Landmann am Flügel vorgetragen, eine halbe Stunde klassische Stücke; dazu zweimal in der Woche zur Abendsprache, oft auch Konzerte.
Dies war der springende Moment, wo wir unsere Ohren spitzten und einübten in die so harmonische, klassische, wundervolle Musik, wie sie wohl niemand anderes so intensiv erleben durfte. Ich kann mich noch gut erinnern, wie wir montags die Ankündigungsprogramme am Anschlag der Hohen Halle studierten und am Sonntagabend die alten Programme sammelten und diskutierten. Da hier wirklich nur ausgesuchte Stücke vorgetragen wurden, konnten wir unbewusst unsere Ohren daran schulen.
Das Jagdhornblasen wurde auch in Holzminden von dem einen oder anderen geübt. Ich hatte meine Hauptübungszeit nach dem Mittagessen und hatte ich mir dafür einen besonderen Übungsplatz ausgesucht. Hinter dem Unterhaus unter dem Fenster des Englischlehrers Egon, der dann immer seine Mittagsruhe machte. Jedes Mal öffnete er das Fenster und bat mich sehr geduldig und höflich, doch etwas weiter in den Solling zum Üben zu gehen, weil er noch Hausaufgaben zensieren müsse.
In den letzten 60 Jahren der Ausbildung, der Lehre, des Berufs und der Familie war die klassische Musik für mich ein Stimulans und eine Seelenspeise. Ein Halt beim Bewältigen der vielen zwischenmenschlichen Probleme und ein Antrieb zur Weiterbildung zum größeren, weiseren oder erleuchteten Menschen. Sie hat geholfen, dem Ziel „eines Tages im Himmel sein zu dürfen“ näher zu kommen.
Am Anfang war das Wort. Wort ist Klang und Klang ist Musik. Also war am Anfang Musik. Aus dieser Folgerung ist harmonische Musik das Lebenselixier das uns hilft groß und stark zu sein um die vielen Aufgaben des Lebens zu meistern, um weiterzukommen, um sich zu bewähren, um weiser zu werden um vielleicht eine Erleuchtung zu erhalten. Was nützt es schwach und mutlos durchs Leben zu gehen, da kann man gleich zuhause hinter dem Ofen bleiben und Däumchen drehen. Als nicht Musiker, als nicht Fachmann möchte ich trotzdem hier alles mir erreichbare zusammentragen, das Musik in unserem Leben ausmacht. Vor Allem, wie uns die Moderne an der Nase herum führt und so tut als ob sie auch einen Lebenssinn hat. Um es mit einem Wort deutlich sagen zu dürfen. Die Moderne hat nur einen zerstörenden, destruktiven, zermürbenden, ungöttlichen Einfluss auf unser Dasein. Im Folgenden zeige ich eindeutig wie uns die harmonikale Musik zum Labsal und Ohrenschmaus werden kann, wenn wir sie richtig auswählen, bewerten und fähig sind zu unterscheiden. Wenn es an Unterscheidungsvermögen fehlt dann müllen wir uns zu bei dem heutigen Überangebot. Dieses unterscheiden kann man nur durch lebenslanges, dauerndes Üben lernen. Wenn wir es einmal begriffen haben dann wird Musik zur ersten Lebensspeise die täglich gepflegt und umsorgt werden muss. So halten wir unseren Geist, unsere Seele in Schuss und machen das Leben lebenswert, auch ohne die Flimmerkiste und die jährliche Reise in den Süden. Musik und Mathematik sind göttliche Brüder, die einander ergänzen und voneinander abhängig sind. Wer Musik verstehen will sollte auch etwas von der Mathematik verstehen.
Musik eine harmonische Übung die aus der Tiefe kommt
Die Geschichte der Musik beginnt mit der Geschichte der Menschheit. Es gab und gibt kein Volk der Erde ohne Musik. Wenn auch die Erstformen der Musik unbekannt sind, so sagen uns aufgefundene alte Musikinstrumente und bildliche Darstellungen Musizierender, dass die Urwurzel aller Musik im Sakralen liegt.
Am Anfang war das Wort. Klang ist Schwingung, verdichtete Schwingung ist Materie. Ohne Mathematik keine Musik, ohne Musik keine Mathematik.
Moral und Musik bestimmen das Leben aller Gemeinschaften seit Anbeginn. Die großen Lehrer Chinas waren die Musikmeister die ihre Schüler lehrten gerecht, milde und verständig zu werden und stark ohne Härte mit Würde ihres Ranges ohne Anmaßung, damit sie sich später im Leben behaupten können. Die Lehren wurden singend in Gedichtform vorgetragen, begleitet von den Instrumenten.
Das älteste Tonsystem ist die Fünfganztonreihe, abgeschaut den damals bekannten fünf Planeten. Die Fünftonreihe konnte auf jedem der zwölf Halbtöne der Skala aufgebaut werden, wodurch 60 Tonarten entstanden, die jede einer kosmischen Kategorie zugeordnet war. Die abendländische Musik hat ihre Besonderheit der Mehrstimmigkeit, dem griechisch-philosophischen Denken und der aus ihr entstehenden abstrakten, ordnenden Mathematik zu verdanken. Musik war wie alle Objekte durch Zahlen beschreibbar. Bei der Rock- und Popmusik spielen neben der Gegenbewegung zur Hauptkultur die besondere Form der Kommunikation zwischen Musikstars und Publikum sowie die wohl evolutionär verankerte Neigung, Moden zu folgen, eine wichtige Rolle.
Musik hat mich geprägt.
Schon zum zweiten Geburtstag am 11. Januar 1940 erhielt ich „Volker“ das erste Musikinstrument eine „Ziehharmonika.“ Überall zerrte ich diese für mich schon recht mächtige Quetsche mit mir herum. Keiner durfte sie anrühren, wie eine Stradivari wurde sie von mir umsorgt. Ob ich ihr nun auch Töne oder Tonfolgen entlockte weiß ich nicht mehr genau.
Als sechstes Kind von sieben wurde ich früh von meiner Mutter mit allen Volks-, Kirchen- und Weihnachtsliedern beschenkt. So kann ich die meisten heute noch auswendig mit den zurzeit fünf Enkeln singen. In der Volksschule wurde nach dem Kriege in der ersten bis vierten Klasse, da wir alle zusammen in einem Raum saßen, mit einem Lehrer auf dem Dorf in Liebenburg Kreis Goslar nicht viel Wert auf Singen gelegt. Wir machten oft Wanderungen in das hügelige Harzvorland und konnten uns an den unterschiedlichen Vogelstimmen erfreuen. Wöchentlich besuchte uns der Spielmann „Augustin“ aus Salzgitter und brachte immer die neuesten Geschichten und Schlager mit, die er uns für ein gutes Mittagessen mit seiner Einmann-Kapelle präsentierte. Meine größere Schwester „Heidi“ nahm mich öfters zur Landjugend in die Wirtschaft „Buchladen“ bei Schladen mit, wo auf dem dortigen Saale nach der flotten Musik eines Schifferklaviers Volkstänze von der jüngeren Generation eingeübt wurden.
Ab und zu ging unser Vater mit uns Kindern nach Goslar ins Konzert wenn gerade ein Gastspiel eines hannöverschen Orchesters gegeben wurde. Beethoven, Bach, Schubert. Vater war vom anstrengenden Arbeitstag auf dem Hof oft so geschafft das er vor der Pause einschlief und wir ihn wecken mussten. Mit 10 Jahren erhielt ich zu Weihnachten das erste Fürst-Pless Horn mit fünf Naturtönen das mich bis heute mein Leben lang begleitet hat.
So sah damals die musikalische Bildung eines in der Natur aufgewachsenen Lausbuben aus. Mit der Sexta im LSH Holzminden änderte sich dieses musikalische herumlungern schlagartig.
Harmonie, künstlerische Veranlagung, Verständnis der Natur sind seit Äonen von Jahren in unseren Uranlagen gespeichert und brauchen nur geweckt zu werden um heute wieder in uns neu aufleben zu können. Carl Gustav Jung nennt es „ Das kollektive Unbewusste“. Es ist ein Erinnern an uralte Erfahrungen, erlebte Tonfolgen, Harmonien, Erlebnisse, Begebenheiten die alle in unseren Erbsubstanzen gespeichert sind. Ein gutes Beispiel ist das hervorragende Musikverständnis östlicher Kulturen wie der Japaner oder Chinesen für unsere westlichen Musiken obwohl sie doch mit ganz anderen Klängen aufgewachsen sind.
Warum finden wir eine Tonfolge harmonisch, weil wir mit einem geübten Ohr die natürlichen Terz, Quint oder Sext Ordnungen und so fort in unserm Innersten spüren.
Musik eine der wichtigsten Stimulanz zur Harmonisierung des Körpers, der Seele und der Stimmung muss man wie alles mit jungen Jahren lernen und üben.
Schon im griechisch-römischen Altertum war man der Überzeugung, dass Töne, Zahlen, Intervalle mit den Himmelsbewegungen zu tun hätten. Die Pythagoreer kannten vier mathematische Wissenschaften: Arithmetik, Geometrie, Harmonik und Astronomie.
Diese vier kehren im Curriculum der mittelalterlichen Hochschulen als Quadrivium zurück: zunächst noch als okkulte Wissenschaften verstanden, später „entmythologisiert“: Arithmetik, Geometrie, Musik, Astronomie. Jeder der Planeten erzeuge bei seiner Bewegung einen einzelnen Ton, so gibt Aristoteles die Lehre des Pythagoras wieder. Er sagt sie bilden eine Harmonie. Ernst Behrend hat diese Sphärenklänge der Planeten für unser Ohr hörbar gemacht. Wer sie hört ist von der Klangfülle überwältigt. „Wo sich aber Sonne und Mond und eine solche Menge so gewaltiger Gestirne mit so rasender Geschwindigkeit bewegten, da müsste unbedingt ein Geräusch von einer über alle Begriffe gehenden Stärke verursacht werden. Das nehmen die Pythagoreer an und ebenso, dass die Geschwindigkeiten infolge der Abstände den Zahlen Verhältnissen der symphonen Zusammenklänge entsprechen. Daher behaupten sie, dass durch den Kreislauf der Gestirne ein harmonischer Klang entsteht. “ Dass wir diesen Klang normalerweise nicht hören, erklärt Phytagoras damit, dass wir diesen Ton schon spätestens seit der Geburt kennen und ununterbrochen hören. Da keine Unterbrechungen durch Augenblicke der Stille einträten, würden wir das tönende Geräusch nicht gewahr. Es ist deutlich, dass diese Charakteristik, dieses Verständnis der Sphärenharmonien schon eine späte Phase der Pythagoreerschule wiedergibt.
Die Entstehung der Töne wird aus ihrer Bewegung erklärt, während eine ältere Stufe der pythagoreischen Schule die Harmonie der Himmelsmusik nicht als ein natürliches Ereignis ansah, sondern für ein mystisches, göttliches Ereignis hielt. Die äußere Bewegung ist für sie eine Folge der inneren Bewegtheit.
Pythagoras sieht die Musik – das heißt hier aber: eine sehr ausgewählte Musik – als ein Erziehungsmittel der Seele an. Damit ist wie der Beschreibung zu entnehmen ist, nicht etwa nur ein Erziehungsmittel der Kinder gemeint, sondern auch der Erwachsenen, insbesondere der seelisch geistig strebenden Menschen, die im Pythagoreer-Bund sich zusammengefunden hatten. Diese Musik dient als Mittel, um die Seelen zu läutern, damit sie auf einen Wege wie dem in „Wie erlangt man Erkenntnisse der höheren Welten?,, (Rudolf Steiner) beschrieben ist , sich vollenden können.
Sphärenklänge an unseres Daseins Grenzen.
In ihren Buch „Der Mensch im Strahlungsfeld von Kosmos, Erde und Umwelt“ scheiben Hans Mayer und Günter Winkelbauer sehr ausführlich über die interessanten Entdeckungen des großen Gelehrten Pythagoras.
Das Monochord, Versuchsinstrument der Pythagoreer R. Haase
„Welche wunderbare schwingende Welt, in der wir leben! Auf unserem Weg durch das Wissen unserer Zeit begegneten wir den kosmischen Energien, die uns umgeben, die uns beeinflussen, die uns krank oder aber auch lebensfroh machen. Hätten wir Ohren, diese Schwingungen zu hören: es müsste das Leben in einem unfassbaren, unendlichem Akkord klingen.
Weise Männer haben vor Tausenden Jahren Zusammenhänge begriffen und postuliert, die erst in der Neuzeit durch die Wissenschaft nachgewiesen werden konnten.
Um den Bogen von jenen Philosophen bis heute zu spannen, müssen wir mindestens bis in die griechische Philosophie zurückgehen. In jene Zeit, in der ein Musikinstrument Mittelpunkt einer Philosophenschule wurde.
Zu den ältesten Instrumenten der Musik gehörten im Altertum die Leier und die Harfe. Um deren Gesetze zu verstehen, benutzte man das Monochord. In der Antike hatte dieses Instrument nur eine Saite und ist dann erweitert worden.
Heute hat es insgesamt dreizehn Saiten, die Zahl ist jedoch nicht zwingend vorgeschrieben. Der Name stimmt dennoch, denn alle Saiten sind auf den gleichen Ton gestimmt. Sowohl mit Fingerzupfen als auch mit einem Geigenbogen kann man die Saiten zum Schwingen bringen.
Ein Steg unter die Saiten geschoben, bewirkt dass immer kürzere Teile der Saiten zum Tönen gebracht werden. Der Ton wird dadurch immer höher. Daraus ergibt sich folgendes Gesetz; Der Ton einer Saite ist umso höher, je kürzer, je dünner sie ist, je stärker sie angespannt und je geringer ihr Gewicht ist“.
David spielt Harfe vor Saul, Rembrandt
Die Bedeutung der Zahlen aus Ernst Bindel „Die geistigen Grundlagen der Zahlen“ 1980 Stuttgart
Das Verhältnis des Menschen zur Zahl hat sich im Verlauf der Geschichte gewandelt. Im Altertum wurden die Zahlen als geistige Qualitäten, im alten Ägypten sogar als göttliche Wesenheiten empfunden, die der Erde und dem Kosmos als ordnende und strukturierende Kräfte zugrundeliegen. Seit der Neuzeit wird die alte Zahlenmystik zum Aberglauben erklärt. Erst seit den bahnbrechenden Arbeiten des Mathematikers Ernst Bindel ist es möglich, das Zahlengeheimnis zu durchschauen und einen neuen, dem Intellekt akzeptierbaren Weg zu den Aussagen der Zahlen zu finden. Jede Zahl ist eine geschlossene Wesenheit, die in sich durch ihren Nennwert differenziert ist, ihre Qualität durch ihre verschiedenen Rechnungsarten kundtut (z. B. Addition, Subtraktion etc.) oder sie im »Gewand« der Fläche und des Raumes sichtbar und im » Gewand « der Musik hörbar macht. Der jeweilige Zählwert der Zahl ist nur ihre Außenseite, ihr Inneres offenbart sie durch die Addition der Weisheit, d. h. durch die Summe ihres von Schritt zu Schritt ansteigenden Wertes (z. B. 3 – I + 2 + 3 = 6), durch die Summe ihrer Teiler (z. B. 8 – 1+2 + 4 = 7) und bei mehrsteIligen Zahlen durch ihre Quersumme (z. B. 11 – 1+ 1 = 2). Der grundsätzliche Unterschied zur alten Betrachtungsweise der Zahlen liegt in der
Zahl EINS, die heute die kleinste Einheit ist, woraus sich alle anderen Zahlen als die Summe entsprechend vieler Einser ergeben. Bis zum Beginn der Neuzeit war die Eins die All-Einheit, die heilige Monade, die Ewigkeit, ein Mutterschoß, aus dem alle anderen Zahlen» geboren« werden, ohne daß die Ureinheit durch Teilung etc. geschwächt wird. Daher wurden alle anderen Zahlen immer im Verhältnis zur Eins gesehen. Die Eins schafft weder Körper noch Raum, sie ist auf eine »unirdische Art« Körper und Raum. Das zeigt sie am deutlichsten mit ihren Symbolbildern, der Kugel und dem Kreis, die beide nicht in derselben Art begrenzt sind wie z. B. der Kubus, der durch sechs Quadrate begrenzt ist. Die Kugel kann sich vom Punkt aus, der selber eine winzige Kugel ist, durch eine zentrifugal wirkende Kraft bis zum unendlich Großen ausdehnen (im Unendlichen verschwinden), um dann durch eine zentripetal wirkende Kraft von der Peripherie her wieder bis zum Punkt zusammenzuschrumpfen. Sie geht dann durch den Nullpunkt, das unendlich Kleine, um den Prozeß von neuern zu beginnen. Ein ewiges» Stirb und Werde«, ein Atemprozeß, der dem Wesen der Zahl Eins entspricht, ohne schon eine» irdische Aktion« zu se111. Diese entsteht erst durch die Heraussonderung der Zwei. Die Pythagoräer nannten
die ZWEI den »Streit «, die »Vcrwegenheit «, denn durch sie entsteht »Aktion«, die sich in Polarität, Opposition, Dissonanz, Hintereinander-Nacheinander etc. zeigt, aber auch in Zweisamkeit, Konsonanz, Nebeneinander etc. (Mann-Weib, Gut-Böse, These-Antithese, Partnerschaft, Ehe usw.). Da die Polarität von Leben und Tod zur Qualität der Zwei gehört, nannte man die Zwei auch die Zahl der Offenbarung der Welt. Durch die Zwei werden alle Zahlen in gerade und ungerade Zahlen unterschieden. Die ungeraden nannte man männliche, die geraden weibliche Zahlen.
Mit der DREI entsteht eine neue, aber nun in sich gegliederte Einheit, die sich am deutlichsten im Dreieck zeigt, der ersten irdisch begrenzten Fläche. Das Dreieck ist nicht nur das Symbolzeichen der Drei, sondern primär das Symbol der sich als Dreieinigkeit offenbarenden Gottheit selbst, die man hinter allen Offenbarungen der Drei suchen muß, z. B. in der dreifach gegliederten » ewig fließenden Zeit « (Zukunft – Gegenwart – Vergangenheit – Zukunft … ). Zudem entsteht durch die )) Dreidimensionalität« der )) unendliche kosmische Raum «. Der erste )) irdisch begrenzte« Raum-Körper, das aus vier Dreiecken gebildete Tetraeder, wird erst durch
die VIER » geboren «. Die Pythagoräer nannten die Vier »die Welt«, denn sie ist die Zahl der heutigen Erde und ihres paradiesischen Uranfangs, was sie dadurch zeigt, daß die Erde aus vier Elementen besteht (das Feurige, das Gasig-Luftige, das Flüssige, das Erdig-Feste) und von vier Himmelsrichtungen umschlossen ist, von vier Reichen bewohnt (Mineral-, Pflanzen-, Tier- und Menschenreich) und von vier Jahreszeiten belebt wird.
Die FÜNF wird die Zahl des Individualismus und der Krise genannt. Beides zeigt sich am deutlichsten an ihrem. Verhalten in der Fläche. Da man im Altertum die verheerenden Folgen des vom Egoismus ausgehenden Individualismus vorausahnte, wurde im exoterischen Bereich vor der Fünf gewarnt, sie galt als Zahl des Bösen. Im esoterischen Bereich Ägyptens und Israels wurde sie gepflegt (Exkurs in das Zahlengeheimnis). Die Fünf ist aber auch die Zahl des Menschen und vor allem die Zahl des »zukünftigen Menschen«. Durch die Fünf entsteht die erste echte Sternform, das Pentagramm, in das sich die Menschengestalt einschreiben läßt. Der Zukunftsmensch wird nicht mehr viergegliedert sein wie der heutige Mensch (physischer Leib – Lebens- oder Ätherleib – Seele oder Astralleib – Ich), sondern als fünfgegliederter Mensch das » Manas oder Geistselbst « dazugewonnen haben. Die
SECHS wird die Zahl der Vollkommenheit genannt. Das zeigt sie sowohl im „ geometrischen Gewand« (ihre Flächenform, das Hexagon, läßt sich aus dem Radius eines jeden Kreises bilden, der jeweils sechsmal in die Kreisperipherie paßt) wie durch die Summe ihrer Teiler, die wieder Sechs ergibt (I + 2 + 3 = 6). Bei den meisten anderen Zahlen ist die Summe der Teiler kleiner als die Ausgangszahl. Bei der Sternform der Sechs, dem Hexagramm, senkt sich ein von oben kommendes Dreieck vollkommen harmonisch in ein ihm von unten entgegenstrebendes Dreieck hinein. Auch das Verhältnis der Sechs zur Fläche ist » vollkornmen« zu nennen, denn sie läßt sich mit Sechsecken lückenlos bis ins Unendliche erfassen.
Die SIEBEN ist die zweite !I vollkommene Zahl «, aber ihre Vollkommenheit ist anderer Natur und nur schwer zu erfassen. Die Sieben ist als Primzahl unteilbar, ihre Flächengestalt, das Siebeneck, ist »unkonstruierbar «, nur durch Annäherung zu finden, auch entzieht sie sich der Fläche und der Körperwelt; dafür bildet sie aber zwei Sterne, von denen der zweite besonders interessant und strahlend schön ist (siehe Exkurs in das Zahlengeheimnis). Die Sieben ist die Zahl der Zeit im Raum, was an ihren beiden Komponenten, der Drei, der Zahl der ewig fließenden Zeit, und der Vier, der Zahl der Erde und des endlichen irdischen Raumes, abzulesen ist, denn wenn die unendliche Zeit in den endlichen irdischen Raum eintritt, entsteht die Zeit als rhythmisches, d. h. individualisiertes WeseIl. Als solches liegt die Sieben u. a. dem Mondenrhythmus, der Metamorphose der Pflanzen und der Entwicklung der menschlichen Biographie zugrunde. Vom Altertum bis zur Neuzeit wurde die ACHT immer für eine lebenspendende, erquickend-heilkräftig wirkende, aufbauende Wesenheit gehalten. Das zeigt sich u. a. in der Addition der Weisheit, die bei ihr die Zahl 36, die große Tetraktys des Pythagoras, ergibt (I + 2 + 3 + … 8 = 36). Sie ist außerdem die Summe der vier ersten männlich ungeraden und der vier ersten weiblich geraden Zahlen (I + 3 + 5 + 7 + 2 + 4 + 6 + 8 = 36). Ihre Quersumme ergibt Neun (3 + 6 = 9). Aus einer Gottheit hervorgegangen und durch acht schöpferische, göttliche Wesen gestaltet (vier männlich/väterliche und vier weiblich/ mütterliche), empfanden die alten Ägypter den gesamten Kosmos entstanden (4 + 4 = 8 + 1 = 9). Aber auch an dem Zahlzeichen der
ACHT, das eine Lemniskate ist, zeigt sich ihre Qualität. Die Lemniskate ist der graphische Niederschlag des »unendlichen Atemprozesses« der Kugel, des Symbols der allumfassenden Eins (siehe Exkurs in das Zahlengeheimnis). In christlicher Zeit wurde die Acht zur Zahl des Christus, insbesondere in seinem Wirken als Heiland, aber auch der Maria. Viele Taufkapellen, Taufsteine und Brunnenstuben haben eine oktogonale Form.
Die NEUN ist ähnlich schwer durchschaubar wie die Sieben. Sie ist die Zahl der Erdentalwanderung, die eine Krise und ihre mögliche Überwindung beinhaltet (siehe Exkurs in das Zahlengeheimnis). Ersichtlich wird diese Qualität an folgendem: Die Neun ist 3 x 3 oder 3 hoch 2. Das zeigt sie an der zweiten ihrer drei Sternformen die aus drei ineinander verflochtenen Dreiecken besteht. Die Summe ihrer Teiler ergibt Vier, die Zahl der Erde (1+3=4). Die Addition der Weisheit ergibt 45 und zeigt damit die beiden wichtigsten Komponenten der Neun, die Vier und die Fünf. Ihre Quersumme ist wieder die Neun (4 + 5 = 9)· In drei Schritten (Abstieg, Durchgang durch die Krise, Wiederaufstieg), ausgehend von der Ureinheit (Eins) über die Qualität der Vier als paradiesischer Erdenanfang (Symbol ist das Quadrat) und über die Fünf, die Qualität des Individualismus, gelangt man zur Neun, der Qualität der großen Krise, die zum Absturz in das Nichts der totalen Gottferne führt, wenn nicht ein Aufstieg zur Qualität der Vier, jetzt der »neuen Welt«, des Neuen Jerusalems der Apokalypse, gefunden wird (Symbol ist der Kubus). Dieser Weg führt wieder über die Fünf, jetzt aber als Qualität des zukünftigen Menschen, zur allumfassenden Eins. Zehn und Zwölf sind Zahlen, die eine »Fülle «. ein »Pleroma « ausdrücken.
Die ZEHN ist die Zahl der irdischen Fülle. Bei Pythagoras ist sie die» kleine Tetraktys «, denn sie ist die Summe der ersten vier Zahlen (I + 2 + 3 + 4 = 10). Ihre Quersumme ist die allumfassende Eins. Durch ihr Dezimalsystem lassen sich alle irdischen Belange, auch die materiellen des Kosmos, mathematisch optimal erfassen. Am deutlichsten zeigt die Zehn ihre Qualität in ihrer Flächenform. Zehn Winkel zu je 36° um den Mittelpunkt eines Kreises gezeichnet, ergeben an dessen Peripherie zehn Punkte, die miteinander verbunden das Zehn eck ergeben. Von einem Gestaltungszentrum aus, einem mikroskopisch kleinen Zehneck in der Mitte, kann sich die Zehn in immer größer werdenden, kreisähnlichen Zehnecken die Fläche bis in die Unendlichkeit erobern. Die dadurch entstehende Form, die zunächst einem. Spinnengewebe zu gleichen scheint, birgt eine Fülle weiterer Formen: Pentagone, Pentagramme, Trapeze (also Vierecke) und Dreiecke (siehe Exkurs in das Zahlengeheimnis).
Die ZWÖLF ist die Zahl der kosmischen Fülle. Die Qualität der Fülle zeigt sie u. a. daran, daß sie die erste der seltenen Zahlen ist, deren Summe der Teiler größer ist als sie selbst (I + 2 + 3 + 4 + 6 = 16). Die Sechzehn ihrerseits ist 2 x 8, ihre Quersumme ist die Sieben (I + 6 = 7). Die Addition der Weisheit ergibt bei der Zwölf 78, mit der Quersumme 15 (3 x 5). Deren Quersumme ist die Sechs (I + 5 = 6), die Zahl der Vollkommenheit, die sich hier zum zweiten Mal zeigt. Es stecken also scheinbar, mit Ausnahme der Neun, alle einstelligen Zahlen, teils direkt, teils virulent, in der Zwölf. Aber auch die Neun ist ganz versteckt in ihr anwesend, desgleichen die kleine und die große Tetraktys (siehe Exkurs in das Zahlengeheimnis). Auch ihre Flächenform, das Zwölfeck, das schon fast wieder ein Kreis ist, zeigt diese Qualität. Ihre kosmische Qualität wird im Duodezimalsystem erkennbar, mit dem sich kosmische Belange mathematisch besser erfassen lassen als durch das Dezimalsystem, ferner in der vierten ihrer vier Sternformen. die einer „ Sonne « gleicht, sowie in ihrem Raumkörper. dem Pentagondodekaeder, der einer Kugel gleicht, der aus zwölf Richtungen des Kosmos zwölf Pentagone eingeprägt werden.
Die DREIZEHN ist als Primzahl wieder schwer zu durchschauen. Ähnlich wie die Elf, die als Zahl der Übertretung der kleinen Tetraktys, der heiligen Zehn, einen ausschließlich negativen Charakter hat (Zahl des Todes), ist auch die Dreizehn als Übertreterin der heiligen Zwölf eine Zahl des Todes, aber dieser Tod hat eine andere Qualität (siehe Exkurs in das Zahlengeheimnis). Die Dreizehn wird auch die Regentin der Zwölf genannt. Das zeigt sich z. B. daran, daß zwölf Tierkreiszeichen von der Sonne, einem Dreizehnten, regiert werden, zwölf Bodhisattwas durch einen Dreizehnten belehrt werden, oder Christus sich mit zwölf Jüngern umgibt. Im Dornröschen-Märchen ist die dreizehnte Fee zwar die böse Fee, weil sie den Todesfluch ausspricht, aber sie spricht ihn nach der elften Fee aus, so daß der Wunsch der zwölften Fee den Fluch in den hundertjährigen Schlaf wenden kann. Nachdem er abgelaufen ist, führt er durch das Erscheinen des Königssohns, des »neuen Prinzips «, zu einem neuen Königtum. Die Dreizehn hat hier die Qualität, die aus dem Tod neues Leben gebiert. Daher vor allem war sie auch immer eine Zahl des Christus.
Mathematische Strukturen in der Musik.
Die Tetraktys, (Vierheit, Schlüssel zum Verständnis der Weltharmonie, 1+2+3+4=10, Dezimalsystem) die den griechischen Tonsystemen zugrunde liegt und die als Quelleund Wurzel ewiger Natur angesehen wird, ist durch die Zahlen 6, 8, 9 und 12 wiedergegeben. Am Monochord, dem Instrument mit einer Saite, wurden diese Zahlen zum Erklingen gebracht, indem die Saite in zwölf gleichlange Abschnitte eingeteilt und Saitenlängen jeweils bestehend aus 6, 8, 9 und 12 dieser Abschnitte abgegriffen wurden. Ist die Saite auf E gestimmt, so ergeben sich dabei die Töne e, H, A und E. Den Intervallen Oktave, Quinte und Quarte wurden deshalb die Zahlenverhältnisse 2 : 1, 3 : 2 und 4 : 3 zugeordnet. Die Oktavaufteilung der Tetraktys war Ausdruck der Lehre vom arithmetischen und harmonischen Mittel: Die Zahl 9 ist das „arithmetische Mittel“ zwischen 12 und 6, d. h. die Differenzen 12−9 und 9−6 sind gleich. Die Zahl 8 ist das”harmonische Mittel“ zwischen 12 und 6, d. h. die Differenzen 12−8 und 8−6 verhalten sich wie 12 zu 6. Alle vier Zahlen bilden die Proportion 12 : 9 = 8 : 6, die in ihrer Verbindungvon arithmetischem und harmonischem Mittel die ”vollkommenste Proportion“ genannt wurde. Folgende Verhältnisse bezüglich des Grundtones c sind am Monochord aufgezeigt:
c f g c Tonbezeichnung
1 4/3 3/2 2 Verhältniszahl
Prime Quarte Quinte Oktave Intervall
„Die Pythagoreer experimentierten mit dem Monochord und variierten die Länge der unter konstanter Spannung stehenden Saite durch Einschieben eines Steges. Beim Halbieren ergab sich ein zum Grundton harmonischer Oberton. Diesem harmonischen Zusammenklang zweier Töne entsprach das Zahlenverhältnis 1 : 2, und in der Musiktheorie bezeichnet man dieses Intervall als Oktave. Es lag nahe, den schwingenden Anteil auf zwei Drittel der ursprünglichen Länge zu verkürzen. Der so erzeugte Ton ergab mit dem Ausgangston einen angenehmen Zusammenklang, der in der Musiktheorie als Quinte bezeichnet wird. Schließlich gaben sie bei ihren Experimenten drei Viertel der ursprünglichen Länge zur Schwingung frei. Der so entstandene Zweiklang hörte sich ebenfalls erträglich an; in der Musiktheorie wird dieses Intervall als Quarte bezeichnet. Ganz allgemein entspricht dem Nacheinander ausführen zweier Tonschritte das Multiplizieren der entsprechenden Verhältniszahlen. „Damit verbunden ist das lateinische „ musica mundalla“ das Pythagoras zugeschrieben wird. Er prägte den »pythagoreischen Lehrsatz. Aber die Formel mit dem Inhalt des Hypothenusenquadrates ist gar nicht seine für die Welt wichtigste Erkenntnis. Sehen wir uns die griechische Geschichte noch ein wenig an. Sprechen wir von Thales von Milet, dem genialen Mathematiker. Er lebte etwa 600 vor Christus und war ein weitgereister Mann, der seine Handelsfahrten zu Studienzwecken benutzte.
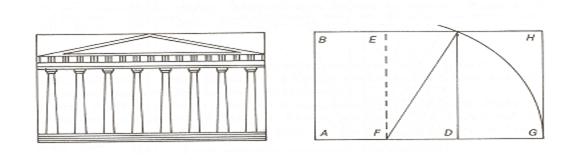
Links: Das Pantheon in Athen passt fast genau in ein go1denes Rechteck (nach A. Brotmann) Rechts: Das goldene Rechteck, gewinnt man indem man ein Quadrat halbiert und den Boden dieses Rechtecks auf die Basis klappt.
Pythagoras, auf Samos geboren, hat möglicherweise mit Thales gemeinsam studiert. Zumindest deuten gewisse gemeinsame Gedankengänge darauf hin.
Wie immer, Thales ließ sich nach seinen »Lehr- und Wanderjahren« in Kroton, einer griechischen Kolonie in Süditalien, nieder. Hier fanden sich im Jahre 540 vor Christus einige weise Männer zusammen, zu denen Thales ebenso wie Pythagoras gehörten. Sie experimentierten mit dem Monochord. Aber auf eine Weise, die mit dem Spielen von Melodien nichts zu tun hatte. Diese Gemeinschaft ist am besten damit beschrieben, dass es sich um einen Orden von halb philosophischer, halb mathematischer Bedeutung handelte. Die Bezeichnung »Orden« ist deshalb gewählt, weil die Männer dieser Gemeinschaft sich geschworen hatten, ihre Erkenntnisse bei sonstiger Todesstrafe geheim zu halten. Aber nichts bleibt so geheim, als dass es – wie in diesem Fall- nicht wenigstens ein Jahrhundert später bekannt wird: Pythagoras hatte die ganzzahligen Relationen der Töne erkannt! Und er ging davon aus, dass alle Harmonie, Schönheit und die Natur in ganzzahligen Relationen ausgedrückt werden können.
Eine der Grundthesen dieses »Ordens« war, dass die Planeten und ihre Bahnen ganzzahlige himmlische Harmonien erzeugen. Eben: »Sphärenmusik«. Zweitausend Jahre später hat das Johannes Kepler astronomisch-mathematisch nachgewiesen.
Nikomachus von Gerasa und Theon von Smyrna sind die Hauptvertreter der Gedanken, die man als »neuphythagoreisch« bezeichnet. Von ihnen und anderen gelangten manche Überlegungen ins Mittelalter. Aber erst in der Renaissance gab es eine Wiederbelebung der Idee von der Weltharmonie.
Der Einfluss des »Harmoniken Denkens« in der Baukunst ist zu beweisen. Es galt in der Gotik als eines der »Bauhüttengeheimnisse« der Dombauherren. Der Nachweis ist dem »Bauhüttenbuch des Villard de Honnecourt« aus dem 13. Jahrhundert zu entnehmen. Johannes Kepler 1571-1630 wollte die Weltharmonie, wie unten so auch oben, nachweisen.
So hat er mathematisch zeigen können, dass sich die Umlaufbahnen der Planeten nahtlos in die Harmoniken Gesetze einfügen! Er hat auch die Keohlerschen Gesetze entdeckt, die heute noch gelten.
Harmonikaler Teilungskanon aus dem Bauhüttenbuch des Villard de Honnccourt,13. Jahrhundert nach R.Gneizer,
Aber mehr noch. Der Schweizer Gelehrte Dr. Hans Kayser (1891-1964) hat die Forschungen Keplers alle bestätigt. In weiterer Verfolgung dieser Recherchen führt uns die harmonikale Grundlagenforschung an die Hochschule für Musik und darstellende Kunst in Wien.
Je schneller der Umlauf des Planeten, desto heller der Klang (Harmonices mundi libri V, 1619).
Die von Johannes Kepler erdachten Sphärenharmonien schrieben den bekannten Planeten jeweils eine Melodie zu. Je schneller der Umlauf der Planeten je heller der Klang.
Professor Dr. Rudolf Haase, ist ein Schüler des Schweizers Kayser und lehrt an seinem Institut die Keplersche Welt-Harmonie.
In der Heilkunst finden wir die »Musiktherapie«. Ebenso weiß man, dass Musik auf das Verhalten der Tiere wirkt. Kühe etwa geben bei einer harmonischer Musik mehr Milch. Blumen wenden sich ab vom Rock und hin zu Mozart.
Im Bereich der Töne wirken alle Frequenzen von 18 bis 10.000 Hertz fördernd, dagegen die von 10.000 Hertz bis zu den Ultraschallwellen hemmen das Wachstum. Dadurch wird erklärlich, dass Ultraschallwellen Samen im Wachstum hemmen, Herzfunktionen stören. Besonders die Nerven der Sinnesorgane im Gehirn, im Rückenmark und jene des Sympathikus werden durch Schallwellen beeinflusst. Folgen wir diesen Feststellungen, dann sind es immer wieder Misstöne wie Motorrad- und Autolärm, Türenschlagen, Martinshörner, Rock und so weiter, die nicht nur stören, sondern ausgesprochen gesundheitsschädlich sind. Das ist an sich nichts Neues. Doch in diesem Zusammenhang ein Nachweis von harmonischer Verirrung. Denn der Mensch ist, wie jedes Lebewesen, ein Instrument, das Schwingungen nicht nur abgibt, sondern auch empfängt – ja von ihnen abhängig ist. Nicht nur der Mensch schwingt. Erinnern wir uns an die »Schumann-Resonanzen«, dass nämlich der Hohlraum-Resonator Erde-Ionosphäre bei der Anregung von Blitzentladungen im Frequenzbereich von 10 Hertz schwingt. Kehren wir jetzt zurück zu den Pythagoreern und ihren Experimenten des Monochords. Die von ihnen gefundene Gesetzmäßigkeiten der Tonintervalle sehen so aus: Wenn bei einer Saite der Steg genau in der Mitte eingeschoben ist, entsteht ein Intervall, das wir unter der Bezeichnung Oktave kennen. Alle Töne, proportionale und Intervalle, sind untrennbar miteinander verbunden. Eine klingende Saite schwingt nicht nur in ihrer gesamten Länge. Sie schwingt auch in den unterschiedlichsten, selbständig schwingenden Teilen. Neben dem Grundton sendet dieses schwingende System noch eine Reihe von anderen Tönen aus, die Obertöne. Und jetzt wird es nicht nur interessant, sondern geradezu mystisch: Diese Obertonreihe ist ident mit jener Ton Reihe, die man erhalten würde, wenn man eine schwingende Saite fortlaufend durch die einfachen ganzen Zahlen teilt.
Die Periode der Teilschwingungen 1/2, 1/3, … n bildet in der Mathematik eine Zahlenreihe, die man „harmonische Folge« nennt. Die Obertonreihe, die bei jedem Klang mitschwingt, ist ein physikalisches bzw. akustisches Grundgesetz. Die Partialtöne bilden diese ganzzahligen Vielfachen der Frequenz des Grundtones:
1/2, 1/3 , 1/4 ,1/5 ,1/6, 1/7, 1/8, 1/9, 1/10 •••• Grundton
C c g c‘ e‘ g‘ b‘ c“ d“ e‘
1 : 2 : 3 : 4 : 5 : 6 : 7 : 8 ; 9 : 10
Cc=1:2= Oktave, cg= 2:3= Quinte, gc’=3:4 =Quarte
c‘e’= 4:5= Große Terz, e’g’=5:6= Kleine Terz
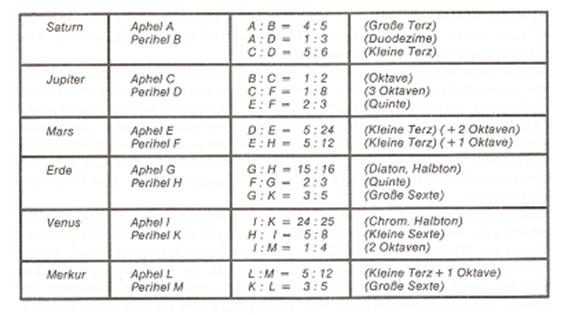
Die Überlegungen der Pythagoreer gipfelten in der Vorstellung, dass in der Natur, in der Musik und im Menschen identische Gesetze existieren. Folgen wir weiter einer phantastischen Entdeckung: Johannes Kepler berechnete die Winkelgeschwindigkeiten der Planeten am sonnennächsten (Perihel) und sonnenfernsten (Aphel) Punkt ihrer Bahnen. Dabei kam ein System ganzzahliger Verhältnisse zutage, das den musikalischen Intervallen entspricht. Hier können wir es uns ansehen:
Intervalle der einzelnen Planeten nach R. Haase
Aus dieser Berechnung geht hervor, was Kepler gar nicht wissen konnte. Es ist heute wissenschaftliche Tatsache, dass die Harmoniken Anteile der Planetengesetze zeitlose Gültigkeit haben. Die Planeten Uranus, Neptun und Pluto, die Kepler noch nicht kannte, fügen sich nahtlos in dieses Gesetz. Mehr noch: 1766 hat Titius eine weitere Gesetzmäßigkeit entdeckt. Schreibt man eine geometrische Reihe, so kann man leicht die Abstände der Planeten daraus ableiten. Hier das Beispiel:
Tabelle der Abstände der Planeten nach J.D. Titius
Weitere Übereinstimmungen: Das periodische System der Elemente in der Physikochemie ist bei der Reihung nach den Ordnungszah len (Elektronenzahlen) ident mit dem Aufbaugesetz der Obertonreihe. Diese Gesetzmäßigkeit finden wir auch in kleinsten Bereichen. Sie ist ebenso gültig auf die Strukturierung des Atoms anzuwenden. Schließlich noch ein Übriges: Auch der Mensch ist mit seinem körperlichen Aufbau nach Harmoniken Gesetzen erschaffen. Als erster hat der Arzt Agrippina von Nettersheim im Mittelalter die Proportionen das menschlichen Körpers nach dem musikalischen Verhältnis Terz-Sext in ein Netz von Kreisen und Dreiecken gezeichnet“.
Agrippina von Nettesheim, Proportionen des Menschen
 |
Kunst der Fuge
Namen, Gedichte oder Psalmen sind oft von Bach oder Beethoven und anderen in die Stücke eingebaut worden. Die letzte Seite des Originalmanuskripts von Bachs Kunst der Fuge, oben, trägt in der Handschrift von Bachs Sohn Carl Philipp Emanuel den Vermerk: „NB. Im Verlauf dieser Fuge, an dem Punkt, an dem der Name B.A.C.H. als Gegenthema eingeführt wurde, starb der Vater. “ (B-A-C-H oben eingerahmt.) Diese letzte Seite von Bachs letzter Fuge soll mir als Denkmal (Epitaph) dienen. (Notensatz durch das von Donald Byrd entwickelte Programm „SMUT“).
Der große chechische, zeitgenössische Komponist Peter Eben schreibt über die Demut des gregorianischen Chorals:
Das, was mich am gregorianischen Gesang oft ergreift, ist – neben dem Inhalt – seine augenscheinliche Demut. Hier kennt der Komponist noch keinen Ruhm, hier arbeitet er wie jeder andere – inmitten einer Gemeinschaft, der er dient, anonym und ohne Originalitätsansprüche. Ein Zauber des gregorianischen Gesanges ist auch der Puls des langsameren Jahrhunderts. Die Hektik unserer Zeit hat auch in die Musik eine gewisse Atemlosigkeit und Hast hineingetragen, wir ergehen uns im schnellen Tempo und vertragen ausgedehnte Flächen nicht mehr. Man schreibt nicht mehr so sehr an stundenlangen Sinfonien, sondern an solchen, die nur Minuten dauern (wie Darius Milhaud), man liest nicht mehr Romane von fünfhundert Seiten. Das Feld beherrschen Novellen, Kurzgeschichten, alles muss möglichst kurz sein. Und gerade deshalb wird auf uns ein solch beruhigender Eindruck ausgeübt, wenn wir plötzlich in einen musikalischen Freiraum geraten, der, aus dem Nichts kommend, sich nirgendwo hinneigt, sondern am Ort stillsteht; eine Musik, die sich gleichsam wie im Kreis bewegt – und, sobald wir ihn betreten, die Zeit anhält und unsere Unruhe stillt.
Manfred Stöhr äussert sich sehr treffend über die Seele und die Kunst in seinem Werk „Der Mensch ist mehr als sein Gehirn„ folgende Überlegungen. Dass sich Seelisches in Stofflichem auszudrücken vermag, zeigt sich nicht nur am menschlichen Leib, sondern auch in der Kunst. Maler und Bildhauer bearbeiten Materie in einer Weise, dass Anschauungen und Gefühle darin aufscheinen, in Formen und Farben gemischt und in Stein gemeißelt. Farben und Formen offenbaren geistige Inhalte wie Liebe und Grausamkeit, Freiheit und Unterdrückung, menschliche Größe und Niedrigkeit, und manches kann dadurch verständlicher ausgedrückt werden als durch Begriffe. Geistige Inhalte werden vom Künstler in das jeweilige Kunstwerk gelegt und erwecken im kunstsinnigen Betrachter gleichartige Empfindungen. Ebenso, wie sich in Haltung, Blick und Mimik Freude und Trauer, Hoffnung und Verzweiflung ausdrücken, schaffen Künstler dasselbe mit ihren Mitteln, so dass beispielsweise Leonardo da Vinci mittels Leinwand und Farben seiner Mona Lisa und Matthias Grünewald dem Isenheimer Altar eine unbeschreibbare geheimnisvolle Aura verleihen konnten. Komponisten erreichen derartige Wirkungen mit ihren Partituren, sofern diese von einfühlsamen Musikern und Sängern interpretiert werden. Dabei ist Musik naturwissenschaftlich gesehen nichts anderes als ein Ineinander von Schallwellen unterschiedlicher Frequenz und Stärke, somit ein rein physikalisches Phänomen. Und dennoch ist in sie unsichtbar und unerklärlich Liebe und Hass, Glück und Traurigkeit, Sinn und Abgründigkeit, Hoffnung und Verzweiflung eingewoben und rührt die Herzen der Hörer. Die Bandbreite der in musikalischen Werken ausgedrückten Gefühle reicht von überschwänglichem Jubel bis hin zu tiefster Trauer, und Menschen, die hierfür taub sind und nur Schallwellen vernehmen, sind im Grunde bedauernswerte Geschöpfe. Das Beispiel Musik zeigt, dass durch den Komponisten eine Übertragung geistiger Inhalte auf die physikalische Ebene möglich ist, ebenso wie deren Rückübertragung auf die Zuhörer – eine zweifache Transformation, unmessbar und doch von unbezweifelbarer Realität.
Bereits die unterschiedlichen Tonarten in Dur und Moll erwecken eine spezifische Grundstimmung die durch „bedeutungstragende musikalische Elemente“ überlagert wird. Wie absurd wäre den Wert einer Musik durch Abzählen zu ermitteln. Ebenso ungenügend wie eine derartige Analyse der Musik ist auch eine auf das Materielle beschränkte Untersuchung des Menschen. Ebenso wie Musik mehr ist als die Gesamtheit der Noten, ein Gemälde mehr als Leinwand und Farben, ein Buch mehr als die Summe seiner Blätter und Buchstaben, ist auch der Mensch mehr als die Gesamtheit seiner 60 Billionen Zellen. Klänge, Bilder, Düfte, Berührungen lösen Emotionen aus, die ihrerseits Rückwirkungen auf körperliche Abläufe besitzen, so dass eine zweifache Transformation vom Stofflichen zum Seelischen und erneut zum Stofflichen erfolgt. Nachdem der Leib die psychosomatische Einheit „Mensch“ nach außen hin repräsentiert, erkennen wir in diesem am deutlichsten die altersabhängigen Veränderungen. Der Mensch als Werdender ist eben dadurch ein sich Wandelnder. Parallel zum lebenslangen Reifungsprozess vollzieht sich ein Gestaltwandel, so dass uns das Antlitz eines alten Menschen viel von seiner Biografie verrät. Paradoxerweise ist die Lebenskraft auch die Ursache des Todes – wenn sie eines Tages erlischt. Tote Materie kann nicht sterben, da sie nie gelebt hat.
Heilige Geometrie
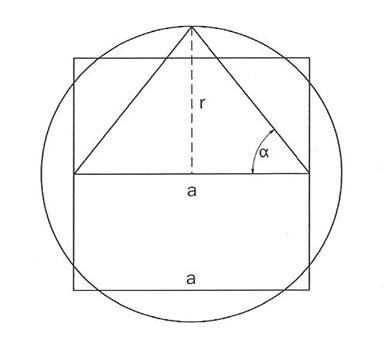
Zur heiligen Geometrie gehören: der „Der Goldene Schnitt“ mit dem Verhältnis: major:minor wie das Ganze zum major, 1:1,618 mit Phi 3,14 für den Kreis, der die göttliche Einheit darstellt; die Eulersche Zahl 2,71 nach der die Natur aufgebaut ist; der Quadratura Circuli mit dem Winkel 51,8540°=51°51‘14“ Steigungswinkel der Pyramiden und des Agnihotra Feuertopfes, Teilung des Siebensterns, Chartre;
Fibonacci-Folge 1,2,3,5,8,13.(Verhältnisse der chromatischen Tonleiter), Primzahlen.
Quadratura Circuli
Aus „Agnihotra“ der Feuerritus von Horst und Birgit Heigl Homa Hof Heiligenberg
Nun ist es erst mal genug mit der hohen Mathematik und kommen wieder auf die Erde zurück in die Schulzeit im Landschulheim Holzminden im Solling wo ich von der Sexta 1949 bis 1954 mit der harmonischen Welt in Berührung kam.
In den folgenden 60 Jahren der Ausbildung, Lehre, Beruf und Familie ist die klassische Musik zu einer Stimulanz, harmonischen Bildung, Seelenspeise, Halt beim Bewältigen der vielen zwischenmenschlichen Probleme, Weiterbildung zum Größeren, weiseren oder erleuchteten Menschen geworden. Sie hat geholfen, das Ziel „eines Tages im Himmel sein zu dürfen“ voranzutreiben. Inzwischen ist eine ausgesuchte Musikbibliothek mit etwa 500 klassischen Kompositionen von 150 Komponisten mein ständiger Begleiter. Das aufmerksame, feine Ohr lernt zwischen passend und unpassend zu unterscheiden. Dies geschieht nur durch ständiges aus- und abwägen, sind alle Harmoniken Gesetze erfüllt, ist es denn nun wirklich ein Seelenschmaus oder nur Verführung dahin oder sogar ein Scharlatan.
| Ort | Komponist | gelebt von/bis |
Stück | Dur/ Moll |
Verz. | Bem. |
| 2 | Albinoni, Tomaso | 1671-1750 | Konzert/Sinfonie/Trompete Oboe | – | – | |
| CD-Li | Trompetenkonzert | D-Dur | ||||
| 95 | Konzert für Violine | G-Dur | Op.10 Nr. 4 | BS |
So könnte man sich eine Datei aufbauen um immer einen klaren Überblick zu behalten, siehe Anhang.
Sprich von Musik nur zu einem Musiker! (China)
Die Offenbarung Gottes in der Zahl zur Harmonieweisheit.
Der Wissenschaftler und Philosoph Rudolf Gorsleben, hat in seinem Buch „Hoch-Zeit der Menschheit“ ausführlich über die Harmonieweisheiten berichtet. Im Folgenden zitiere ich die interessanten Stellen daraus. „Die unsichtbare Achse des Göttlichen, die geistige Irminsul, (Sakral Symbol unserer Mütter und Väter der Germanen) steht senkrecht, das Stoffliche aber ist eine Abweichung vom Geistigen, vom Senkrechten. Ein durchaus ähnliches Bild ergibt sich, wenn wir uns das Weltall als einen Kreis denken. Würden wir die Erdachse einzeichnen, so wiche sie von einer Senkrechten, durch den Kreis gelegt, um 23° ab. Das ist aber der vierte Teil eines Kreisviertels nach nebenstehender Figur.
Durch die Zeitsenkrechte im Kreise gewinnen wir ein Vor und ein Nach, Vergangenheit und Zukunft, ein Positives und ein Negatives, durch die Raumwaagerechte im Kreise ein Oben und eine Unten.
Wir erhalten aber so auch 4 Kreisviertel, die sich gegenseitig entsprechen und die wir nach Maßgabe der Abweichung der eingezeichneten Erdachse von der Senkrechten jeweils in 4 Abschnitte auf den Viertel-Kreisbogen teilen, so dass wir 16 Kreisabschnitte erhalten, oder je 2 acht – geteilte Halbkreisbogen, die sich wie oben und unten, oder wie rechts und links, oder wie positiv und negativ, entsprechen.
Die Erdachse teilt nun aber infolge ihrer Abweichung um 23° von der Senkrechten die Halbkreisbogen in zwei ungleiche Hälften, und zwar nach der Richtung ihrer Abweichung nach rechts in eine kleinere mit drei positiven Teilabschnitten und eine größere Hälfte mit fünf negativen Teilabschnitten.
In diesem Abweichungsverhältnis liegt nun verborgen das mathematische Wunder vom goldenen Schnitt, in dem ein kleinerer Teil zum größeren Teil sich verhält wie der Größere zu beiden zusammen.
In Zahlen ausgedrückt ist es wieder das Verhältnis in der Schöpfung, das sich die Drei verhält zur Fünf wie die Fünf zur Acht oder zum Ganzen.
Die Acht erscheint hier wieder in der Bedeutung des Ganzen, das in die hohe, heilige Acht genommen werden soll bei allem Schaffen und Schöpfen. Im goldenen Schnitt sah die schöpferische Menschheit von je das Verhältnis einer absoluten Harmonie, und für das Endliche, Stoffliche mag dieses Gesetz Geltung behalten. Da aber das Verhältnis des goldenen Schnittes ein Ergebnis der irdischen Abweichung ist von der mathematisch-göttlichen Geraden, Senkrechten, so bestätigt es die Unhaltbarkeit alles Irdischen, Stofflichen als eines Zustandes, der wieder nach seiner Auflösung verlangt im Geistigen, in Gott, denn wir entdecken in dieser furchtbaren Gewissheit irdischer Abweichung von der geistigen Wirklichkeit, der Senkrechten, die entsetzliche Bedeutung einer solchen falschen, ungleichen Harmonie, die eigentlich 4:4 sein müsste und im Göttlichen tatsächlich 4:4 oder absolut ist. Wir dürfen füglich voraussetzen, dass auch die Weltachse ihrerseits wieder eine Abweichung von der göttlich-geistigen Senkrechten aufweist, und das ist für alle Materie gesetzlich gültig. Von dieser Abweichung vom Göttlichen, Senkrechten wiederum haben alle Erscheinungen, Schöpfungen im All ihre polaren Gegensätzlichkeiten im geistigen Positiven und im stofflich Negativen. Stünde die Weltachse, bildlich gesprochen, senkrecht, so wäre wohl alle Erscheinung aufgehoben, nichts wäre möglich, nichts Erschaffenes vorhanden.
Das Ergebnis dieser Abweichung vom Göttlichen, Geistigen, Absoluten ist es, was wir Leben nennen.
Es ist das „Viertel“, von dem seit einigen tausend Jahren die Rigg-Veda (Rigg-Edda) singt:
So groß ist diese, seine Majestät, (Purusha)
Doch ist er größer noch als sie erhoben;
„Ein Viertel“ von ihm alle Wesen sind,
„Drei Viertel“ von ihm sind unsterblich droben.
„Drei Viertel“ von ihm schwangen sich empor,
„Ein Viertel“ wuchs heran in dieser Welt,
Um auszubreiten sich als „alles“
Was durch Nahrung sich und ohne sie erhält.
Platons Einheit und Vielheit
Vor 2500 Jahren ging Pythagoras‘ Vermächtnis auf eine andere tragende Säule der westlichen Zivilisation über: auf Platon, der um 428 v. Chr. geboren wurde, etwa siebzig Jahre nach dem Tod des Pythagoras. In seinem Buch „Harmonie“ schreibt Prinz Charles folgendes: „Platons Werk ist so bedeutend, dass nach Auffassung vieler heutiger Gelehrter alle nachfolgenden Philosophen seinem umfassenden Wissen wenig mehr hinzuzufügen hatten und haben als ein paar Fußnoten. Platon war ein Schüler des Sokrates in Athen und vertiefte sich in das Studium zeitloser Wahrheit. Nach seiner Meinung gibt es eine essenzielle Beziehung zwischen der Mannigfaltigkeit des Lebens, das um uns herum summt und brummt, und der Einheit des ganzen Universums, das diese Vielheit erhält.
Platon behauptete, das höchste Studium überhaupt sei das Studium der Harmonien in der Musik und der Verhältnisse in der Geometrie, denn diesen entsprächen auch die Grundmuster innerhalb der Menschheit. Er lehrte, ohne die Ausgewogenheit des Ganzen, können sich weder Werke der Kunst noch das Leben selbst auf eine dauerhafte und gesunde Art erhalten. Je mehr ein System aus dem Gleichgewicht kommt, so Platon, umso radikaler fallen die Versuche aus, einen Ausgleich herbeizuführen, bis das ganze System ins Wanken gerät und zerfallt.
Mandel einer Kathedrale Geometrische Mandel
Wenn man eine Gerade quer durch die Mitte der Mandelform zieht und ihre beiden Enden mit den oberen oder unteren Kreisschnittpunkten verbindet, entsteht ein vollkommenes gleichseitiges Dreieck. Diese Form ist in der Geometrie von entscheidender Bedeutung, nicht zuletzt deshalb, weil sie eine der tragfähigsten Formen der Architektur ist. Platon sprach in diesem Zusammenhang vom schönsten aller Dreiecke.
Aus einem gleichschenkligen Dreieck lässt sich ein Quadrat konstruieren, und Quadrat und Dreieck ergeben zusammen ein Rechteck, das ebenfalls durch alle Zeiten hindurch eine tiefe symbolische Bedeutung hatte und seit Langem als »Goldenes Rechteck« oder Goldener Schnitt bekannt ist, weil das Verhältnis seiner beiden Seiten 1: 1,618 … beträgt. Im 20. Jahrhundert gab ihr der amerikanische Mathematiker Mark Barr den Namen Phi. Phi ist der erste griechische Buchstabe im Namen eines Bildhauers, des Phidias, dessen Werke im Parthenon hoch oben über Athen ausgestellt wurden und wie der Parthenon selbst ihre Schönheit und Ausgewogenheit aus dem Verhältnis 1: 1,618 … bezogen, das bei ihnen Anwendung fand. Die Griechen nannten es die »Goldene Mitte« oder den »Goldenen Schnitt« er ist in jüngster Zeit durch Bücher und Filme wie den Da Vinci Code, Sakrileg populär geworden. Selbst in etwas so Kleinem und Gewöhnlichem wie dem Blütenköpfchen eines Gänseblümchens ist dieses Verhältnis zu erkennen.
Gänseblümchen
Der Blütenstand mit den Samen des Gänseblümchens bildet zwei durchaus nicht zufällige, sich von innen nach außen drehende Spiralen. Die Spirallinien drehen sich in entgegengesetzter Richtung und folgen einem präzisen mathematischen Größenverhältnis. Die Anzahl von Samen auf der Linie, die in die eine Richtung dreht, entspricht in einer bestimmten Proportion der Samenzahl der in die Gegenrichtung drehenden Samen, nämlich genau im Verhältnis des Goldenen Schnitts.
Die Zahlenfolge, die dieses Verhältnis beschreibt, 1,2,3,5,8,13, ist seit Jahrhunderten als Fibonacci-Folge bekannt und nach dem italienischen Mathematiker Leonardo von Pisa 1170-1240 benannt, der eine lange Studie darüber durchführte, wie sich die Zahl von Kaninchen mit jeder Generation erhöht. Er stellte fest, dass die Vermehrung der Kaninchen in einer Sequenz erfolgt, die genau der Reihenfolge entspricht, in der Pflanzen neue Blätter treiben oder Bäume neue Äste bilden. Den Anfang bildet ein Paar, aus dem dann zwei Paare hervorgehen usw. Da die Tragezeiten der Paare unterschiedliche Folgen bilden, ergibt sich eine merkwürdige Vervielfachung von 2 auf 3 auf 5 auf 8 auf 13 usw. Die Beziehung zwischen den Folgeglieden ist enger, als es auf den ersten Blick scheint. Jedes ergibt sich aus der Addition der bei den vorherigen. Noch weniger fällt ins Auge, dass jede dieser Zahlen, wenn sie durch die vorhergehende geteilt wird, mit stets zunehmender Genauigkeit die bekannte »goldene Zahl« 1,618 … ergibt, eine Zahl, die Johannes Kepler als »kostbares Juwel« bezeichnete. Die Fibonacci-Folge hat eine gewisse Eleganz. Wenn jede der Zahlen die Seitenlänge einer Folge von Quadraten bildet, von denen jedes eine Seite mit dem vorhergehenden Quadrat teilt, entsteht eine Folge von benachbarten Quadraten. Wenn man die Ecken dieser Quadrate mit einer durchgehenden stetigen Linie verbindet, ergibt sich die wohlbekannte Spiralform, die nicht nur bei den Samen im Blütenköpfchen des Gänseblümchens vorkommt, sondern überall in der Natur, etwa im Schneckenhaus oder in der Form, die der Zeigefinger bildet, wenn wir die Hand zur Faust ballen. Immer sind die gleichen Zahlenverhältnisse im Spiel. Jedes einzelne Glied des Fingers von der Spitze bis zur Wurzel ist nach der FibonacciFolge proportional zum nächsten Fingerglied, ebenso wie die übrigen Körperproportionen – von der Nase bis zum Hals, vom Hals bis zur Brust und so weiter. Selbst bei unserem Wachstum spielen diese Zahlen eine Rolle. Unsere Zähne zum Beispiel wachsen entsprechend der allgemeinen Sequenz 1, 2, 3, 5, 8, 13“.
Auch bei Kompositionen spielt der Goldene Schnitt eine große Rolle. Man kann nicht nur Töne nach dem Goldenen Schnitt anordnen (also ihre Frequenzen im Verhältnis von Phi wählen), sondern auch die Teile einer Komposition nach dieser besonderen Proportion bestimmen. Eine solche Komposition finden wir beim ungarischen Komponisten Bela Bartok (1881 – 1945) in dessen Sonate von 1938 (siehe Bild oben). Nicht nur die Länge der drei Teile Root, Position und Inversion stehen im Verhältnis des Goldenen Schnitts, auch Harmonie- und Melodiebildung basieren darauf.
Bekenntnis zu Johann Sebastian Bach vom Urwalddoktor Albert Schweitzer
Was mir Bach ist? Ein Tröster. Er gibt mir den Glauben, dass in der Kunst wie im Leben das wahrhaft Wahre nicht ignoriert und nicht unterdrückt werden kann, auch keiner Entscheidungshilfe bedarf, sondern sich durch seine eigene Kraft durchsetzt, wenn seine Zeit gekommen. Dieses Glaubens bedürfen wir, um zu leben. Er hatte ihn.
So schuf er in kleinen engen Verhältnissen, ohne zu ermüden und zu verzagen, ohne die Welt zu rufen, dass sie von seinen Werken Kenntnis nähme, ohne etwas zu tun, sie der Zukunft zu erhalten, einzig bemüht, das Wahre zu schaffen.
Darum sind seine Werke so groß. Sie predigen uns: stille sein, gesammelt sein. Und dass der Mensch Bach ein Geheimnis bleibt, dass wir außer seiner Musik nichts von seinem Denken und Fühlen wissen, dass er durch keine Gelehrten- und Psychologenneugierde entweiht werden kann, ist so schön. Was er war und erlebt hat, steht nur in den Tönen. Es ist das Erleben aller derer, die wahrhaft leben: Lebensfreude und Todessehnsucht, unvermittelt eins in einem reinen Willen. Die, welche ihn verstehen, wissen nicht, ob es seine Realistik oder seine Mystik ist, die sie so ergreift. Es liegt etwas so unendlich Lebendiges und unendlich Abgeklärtes in seiner Stimmführung. Das ist keine Technik mehr, sondern Weltanschauung, ein Bild des Seins. Jede einzelne Stimme ein Wille, eine Persönlichkeit, alle frei, in Freiheit sich begegnend, sich meidend, sich hassend, sich liebend, sich helfend und zusammen etwas einheitlich Lebendiges, das so ist, weil es so ist.
Gedanken zur Musik
Wir halten die klassische Musik für den Inbegriff unserer Kultur, weil sie ihre deutlichste Äußerung ist. Wir besitzen in dieser Musik das Erbe der Antike und des Christentums, einen Geist heiterer und tapferer Frömmigkeit, eine unübertreffliche ritterliche Moral.
Zwischen 1500 und 1800 ist mancherlei Musik gemacht worden, Stile und Ausdrucksmittel waren höchst verschieden, aber der Geist ist überall derselbe. Immer ist die menschliche Haltung, deren Ausdruck die klassische Musik ist, dieselbe. Immer beruht sie auf derselben Art von Lebenserkenntnis und strebt nach derselben Erhabenheit über den Zufall. Ob das nun die Grazie eines Menuetts von Händel ist oder die zärtliche Sinnlichkeit wie bei vielen Italienern oder bei Mozart, oder die stille gefasste Sterbensbereitschaft wie bei Bach. Es ist immer ein Trotzdem, ein Todesmut, und ein Klang von übermenschlichem Lachen darin, von unsterblicher Heiterkeit. So soll es auch in unserem ganzen Leben, Tun und Leiden klingen. Josef Knecht
Was einem gefällt ist natürlich Geschmackssache. Trotzdem stößt man immer auf besonders charakteristische Stücke mit einem starken Thema wie zum Beispiel:
Albinoni, Tomaso 1671, Violinkonzert G-Dur Op. 10 Nr.4
Bach, Carl Philip Emanuel 1714, Sinfonie F-Dur Nr.3
Bach, Johann Sebastian 1685 Toccata und Fuge D-Moll
Beethoven, Ludwig van 1770, Violinkonzert D-Dur Op. 61
Bellini, Vincenco Konzert s-Dur
Bieber, Heinrich Ignatz Franz 1614, Sinfonie für Violine und Basso Kontinuo F-Dur Nr. 3
Boeliy, Jean François 1739, Konzert für Harfe C-Dur
Bruch, Max 1838-1920 Violinkonzert Nr.1 g-Moll Op. 26
Cimarose, Domenico 1749, Sinfonie für Flöte G-Dur
Corelli, Arcangelo Concerto grosso Nr. 12 f-Dur
Da Labaco, Evaliste F. Koncert f Dur Nr.6 / 6
Dusec, Frantisek 1731, Symphony S-dur
Geminiani, Francesco 1680, Concerto Grosso Violine G-moll Nr.12
Gretriy, Andre Ernest Mordest 1741, Sinfonie G-Dur Op. 3
Händel, Georg-Friederich Overture zur Ode des Alexanderfest
Heyden Michael Perga 33 a-Dur
Leclair, Jean Marie 1697, Violinkonzert C-Dur Op. 73
Mao, Anton Sinfonie Nr.4 C-Moll
Mendelssohn Bartholdy, Felix 1809-1847, Violinkonzert E-Moll Op. 64
Mozart, Vater Leopold Divertimento B-Dur und D-Dur,
Mozart, Amadeus Sinfonie d-Dur Köchel 81
Paganini, Nicolo 1782, Violinkonzert Nr.2 H-Moll Op. 7
Rossini, Giotani 1792, Sonate A-Dur Nr. 2
Scarlatti, Dominico 1685, Concerto Grosso a-Dur Nr. 1
Schubert, Franz Sinfonie Nr.5 d-Dur
Strauß, Richard Hornkonzert S-dur, Walzer Rosenaus dem Süden
Telemann, Georg Phillip Overture g-Dur
Viotti, Antonio Konzert Nr.22 A-moll
Vivaldi, Antonio 1678, Flötenkonzert D-Dur, Op.10 Nr.3 Il Gardellino, Der Distelfink, Concerto Nr.1-4, E-Dur, g-Moll, F-Dur, f-Moll, Vier Jahreszeiten, Concert Grosso C moll für Streicher, Koncert G-moll Op. 10 la notte.
Alle Kompositionen folgender Komponisten sind ohne Ausnahme ein harmonischer Ohrenschmaus:
Johann Sebastien Bach 1685, Wolfgang Amadeus Mozart 1756, Antonio Vivaldi 1678, Georg Fridrich Händel 1685, Joseph Hayden 1732, Robert Schumann 1810, Franz Schubert 1797, Georg Philip Telemann 1681, Nicolo Paganini 1782.
Jeder junge Mensch wird heute von Musik berauscht. Workman oder Handy mit zwei Strippen zu den Kopfhörern ist In. Wie einfach macht es uns die Technik, harmonische Musik von den Medien herunterladen und auf Workman oder Handy kopieren. Alles zum Nulltarif. Auch kann man so Vokabeln oder Gedichte, Lieder, Vorträge, Reden oder sogar Tonfolgen auswendig lernen.
Bedeutung der Notation
Nur in der abendländischen Musik hat sich ein Notenschriftsystem entwickelt, das die eindeutige Abbildung von Tonhöhe, Ton Länge, Rhythmus und Mehrstimmigkeit ermöglicht. Damit wurde Gleichheit zwischen Notenschrift und gespielter Musik hergestellt. Temperatur (Stimmung) ist auch ein Anliegen anderer Musikkulturen, aber ihre mathematische Durchdringung half in der abendländischen Musik, mit der komplexer werdenden Mehrstimmigkeit fertig zu werden, während sie sich z. B. in China und Indien auf Melodieinstrumente bezog. Zur wohlklingenden Mehrstimmigkeit und zu der einfachen ästhetisch ansprechenden Melodik tritt noch ein weiteres wichtiges Merkmal: die Akkorde erhalten eine syntaktische Funktion in der Musik, die ihren Verlauf durch Spannung und Lösung dramatisieren. Die Attraktivität und emotionale Wirkung abendländischer Musik hat wesentlich mit dieser neuen „Sprache“ der Musik zu tun.
Was macht eigentlich unsere Musik zur Musik? Es sind nicht die Töne nach der Tonleiter, sondern das, was zusätzlich als Zugabe mitschwingt, denn wenn wir eine Saite auf der Geige streichen, tönt nicht nur die angeregte Hälfte, sondern auch die anderen tönen mit. Hier vernehmen wir die Obertöne, die vornehmlich, unsere Musik, ihre Erhabenheit, Harmonie und Schönheit ausmachen.
Dieses Schwingen und Quieken im Hintergrund, das in den östlichen Musiken immer zum Vorschein kommt wird bei uns häufig unterdrückt. Wir sind Verstandesmenschen, unser
Gefühl hat uns verlassen, darum wollen wir auch Musik wie Zahlen haben … eins, zwei, drei. Aber alles, was drum herum ist, schneiden wir mit dem rechten Pedal ab.
Das gleiche in der Malerei. In dem Bild von Leonardo da Vinci „Mona Lisa“, das wir so hoch verehren, ist dieses Ungenaue, dieses nicht ganz klare deutlich hervorgehoben. Wir nennen es „sfumato“ die Übergänge verschwimmen lassen. Erst dann kommt wirkliche Malerei, Musik oder wirkliches Leben zum Zuge.
Jeder, der den Namen „Künstler“ mit Recht führen will, muss die ganze Wahrheit der Natur ausdrücken, nicht nur die äußere, sondern vor allem ihre innere. (Rodin-Gsell)
Volltönenden Gedanken
Folgende volltönenden Gedanken hat der große Schriftsteller Hermann Hesse erdacht und für uns festgehalten.
„Dass aus Blättern voll von Notenzeichen solche weitgeschwungenen geistdurchsonnten, solche Welt- und Sternenchöre werden konnten, dass ein Orgelpfeifenchor sie in sich banne, ist es nicht ein Wunder ohne Gleichen. Dass ein Musikant am Manuale sie mit eines Menschen Kraft umsponnen, dass ein Volk von Hörern sie verstehe, miterschwinge, töne, miterstrahle, mit hinauf ins tönende Weltall wehe. Arbeit war’s und Ernte langer Zeit, zehn Geschlechter mussten daran bauen. Hundert Meister fromm es zubereiten, viele tausend Schüler sie begleiten. Und nun spielt der Organist, es lauschen in Gewölben Seelen hingegangener, frommer Meister, mit vom Bau umfangener Geister, den sie gründen halfen und errichten. Das Vollkommene aber ist hienieden ohne Dauer. Krieg wohnt jedem Frieden heimlich inne, und Verfall dem Schönen. Orgel tönt, Gewölbe hallt, es treten neue Gäste ein, verlockt von Tönen eine Frist zu rasten und zu beten, doch indes die alten Klanggebäude weiter aus dem Pfeifenwalde streben voll von Frömmigkeit, von Geist, von Freude, hat sich draußen dies und das begeben, was die Welt verändert und die Seelen.
Kölner Dom 1248-1880 Gotik
Andere Menschen sind es, die jetzt kommen, eine andere Jugend wächst heran, Ihr sind die frommen und verschlungenen Stimmen dieser Weisen nur noch halb vertraut ihr klingt veraltet und verschnörkelt was noch eben heilig war und schön. In ihrer Seele waltet neuer Trieb, sie mag sich nicht mehr quälen mit den strengen Regeln dieser greisen Musikanten, ihr Geschlecht ist eilig, Krieg ist in der Welt, und Hunger wütet. Kurz verweilen diese neuen Gäste hier beim Orgelklang, zu wohlbehütet finden sie, zu priesterlich gemessen die Musik. So schön und tief sie sei. Sie wollen andere Klänge, feiern andere Feste, fühlen auch in halb verschämter Ahnung dieser reich gebauten, hoheitsvollen Orgelchöre unwillkommene Mahnung, die so viel verlangt.
Kurz ist das Leben und es ist nicht Zeit sich hinzugeben so geduldig komplizierten Spielen, übrig bleibt im Dome von den vielen die hier zugehört und miterlebt fast keiner, immer wieder einer geht von hinnen, geht gebückt ward älter, müde, kleiner, spricht vom jungen Volk wie von Verrätern, schweigt enttäuscht und legt sich zu den Vätern.
Niemand weiß ob noch der alte Meister drinnen spiele ob die zarten, die leisen Tongeflechte, die im Raume kreisen nur noch Spuk sind überbleibender Geister. Nachhall und Gespenst aus anderen Zeiten. Manchmal aber bleibt ein Mensch beim Dome lauschend stehen, öffnet sacht die Pforte, horcht, erkennt die fernen Silbertöne der Musik, vernimmt aus Geistermunde heiter ernster Väterweisheit Worte, geht davon mit klangbeschwungenem Herzen, sucht den Freund auf, gibt ihm flüsternd Kunde vom Erlebnis der entrückten Stunde dort im Dom, beim Duft erloschener Kerzen.
Und so fließt im unterirdisch Dunklen ewig fort der heilige Strom, es funkeln aus der Tiefe manchmal seine Töne, wer sie hört spürt ein Geheimnis walten sieht es fliehen, wünscht es festzuhalten, brennt vor Heimweh, denn er ahnt das Schöne. Was wir in unserer Alltagssprache Musik nennen ist nur ein miniaturhafter Ausschnitt aus der Musik und der Harmonie des Universums, die hinter allem wirkt, und die die Quelle und der Ursprung der Natur ist. Viele Religionen der Welt haben uns gelehrt, dass der Ursprung der Schöpfung Klang ist. Die Musik des Universums ist der Hintergrund jenes so viel kleineren Phänomens, das wir auf dieser Erde als Musik empfinden. Unser Gefühl für Musik, die Art in der sie uns anspricht, zeigt uns, dass die wahre Musik in der Tiefe unseres Seins liegen muss. Musik ist im Wesen des Universums. Musik ist nicht nur das eigentliche große Objekt des Lebens, sie ist dieses Leben selbst“.
Mozarts Musik „Eine Entrückung selbst“ von einem der bedeutendsten deutschen Komponisten Hans Werner Henze. Der herabgestiegene Gott. Apollo. Hier ist die Reinheit, das Geglückte. Hier ist die reine Begeisterung des Geistes, die Überwindung der Schwerkraft. Nichts Revolutionäres: alles Vorhandene wurde mit leichter Hand entfremdet und erhöht. In seinem zeitlich so begrenzten Aufenthalt auf dieser Erde hat er die steifen zerebralen Mechanismen, die Sprachmittel seiner Epoche, bis zum Zerbrechen gespannt und ihrem Ende nahegebracht, mit den feinsten, herbsten, tiefsten und höchsten Klängen, die ein menschliches Ohr vernommen hat, dem Leichtesten und Schwermütigsten – mit dem schweren, süßen Wohllaut der Bläser Sätze, mit unendlich feinem Muskelspiel der Streicher, den vollkommensten Vokalensembles, mit hellen triumphierenden Trompeten und Pauken. Was triumphiert? Das Leben über den Tod? Der Tod über das Leben? Es ist der antike Triumph der Schönheit über das Unzulängliche, da das Unerreichbare erreichbar wurde, Vollkommenheit sich über das Leben erhebt mit dem Flügelschlag des apollinischen Todes. Die Form berauscht sich an sich selbst: Das Menschlichste, Humanste, was die Musik hervorgebracht hat, wie man sagt, wird von Schwäche, dem Menschlichen an sich, niemals berührt: Da, wo es scheint, dass Menschliches vorgeht, ist es doch wieder die Form an sich, die Musik selber, die den Rausch empfängt, die das Menschliche auffängt, abfängt, abrückt in die schönste Erhöhung, in die glücklichste Form und vielleicht ist es gerade deswegen, dass so viel Freude sich ausbreitet, weil diese Musik gegen das Sterb liche so ganz abgeschirmt, weil sie die Entrückung selbst ist.
Betrachtungen über die Musik und Kunst
Harmonische Musik ist die Darbietung der Tonfolgen nach göttlichen immerwährenden Gesetzen. Da, wo diese immerwährenden Wahrheiten von Harmonie und Einheit durchbrochen werden, hört die harmonische Musik auf. Sie wird dann künstlich, atonal, naturfern, schädlich, teuflisch, destruktiv.
Unsere Moderne ist, wie es die „Frankfurter Schule“ mit dem Sozialpsychologen Max Horkheimer vorgegeben hat, destruktiv, zerstörend. Die moderne Kunst ist künstlich von oben gemacht. Wenn ich mir eine Komposition von Bach oder Mozart anhöre, dann erlebe ich Freude, Hochgefühl, Ruhe, Natur, eigentlich das, was ich in unserem hektischen Leben heute brauche, um abzuschalten, um ruhig zu werden, um Mensch zu sein. Wenn den ganzen Tag über Telefone klingeln, Sirenen heulen, die Johanniterwagen mit Martinshorn draußen vorbeirasen, dann braucht man Ruhe. Und wenn ich das nur in Form der schönen, harmonischen Bilder bekomme oder einer klassischen Musik, Mozart, Beethoven, oder einer Plastik eines griechischen Kopfes. Dann bin ich beruhigt und habe keine Sorgen mehr.
Aber die Moderne ist genau das Gegenteil, sie reizt, sie macht mich fertig, sie bringt mich zum Wahnsinn, will kämpfen, sie will mich animieren, sie sagt mir jeden Tag, ich verstehe sie nicht, ich bin zu doof, ich muss dran arbeiten, müsste ich? Wenn ich in einem modernen Konzert der Komponisten Schönberg oder Stockhausen bin, halte ich mir die Ohren zu, weil ich diese Katzenmusik nicht aushalten kann. Ich werde noch gereizter als ich schon bin. Das wirkt so auf mich, dass ich zuhause alles kaputtschlage, die Kinder anbrülle, verrückt werde, und darin liegt auch ein Sinn. Wenn ich den großen russischen Maler Kandinsky als Führer dieser Moderne ansehe, dann kann ich den Zeitpunkt „Alte Kunst-Moderne Kunst“, gut erkennen. gemalt um auszuruhen, um sich zu erfreuen, und ab 1905 (Erste russische Revolution) wird es abstrakt, da wird es zerrissen, gereizt, wird es bewusst zum Grübeln, zum Nachdenken, zum Aufputschen.
Kandinsky, Franz Marc, Cézanne, Klee gehörten damals zum Kreis der Blauen Reiter.
Denn nichts anderes als Schwingungen sind die Töne – ein ewiges Hin- und Her tanzen kleinster Luftmoleküle, deren Bewegung erst die Qualität dessen bestimmt, was an die Ohren der Welt dringt.
Das Ohr hat sich den „Klängen, die es aus der Natur kennt, angepasst“. Auch die – letztlich willkürliche – Einteilung der Oktave in zwölf jeweils gleich weit voneinander entfernte Halbtöne in der abendländischen Musik ist schlüssig, weil sie den natürlichen Klangerfahrungen so gut wie irgend möglich gerecht wird.
Dennoch spielt die Mathematik in der Musik schon deshalb eine wesentliche Rolle, weil sie sich zwangsläufig im Rhythmus wiederfindet, der jedes Lied vorwärts treibt. Im Marsch wird das starre Korsett des Viervierteltakts besonders deutlich. Mit der Präzision eines Uhrwerks drehen sich die Derwische im Tanz. Der Walzer ist deshalb so schwungvoll, weil ihn sein Dreiertakt mit Macht im Kreise dreht.
Besonders ergreifend wird Musik jedoch gerade dann, wenn sie mathematisch unscharf (sfumato) wird und sich gleichsam gegen einen allzu starren Rhythmus auflehnt. Ein faszinierendes Beispiel hierfür liefert der Swing: Swing ist das Herz des Jazz. Er erst erweckt Jazzmusik zum Leben und macht den Unterschied zwischen solcher Musik, die einen kalt lässt, und solcher, bei der jeder Fuß mitschwingen muss. Doch wann swingt Musik? Die Grundstruktur des Swing-Rhythmus besteht darin, die Achtelnoten der Musik abwechselnd lang und kurz zu spielen.
Claude Debussy komponierte mit der sechsstufigen Ganztonleiter. Damit schuf Debussy Harmonien, die sich radikal von denen Bachs, Beethovens oder Brahms unterschieden.
Auf die Spitze trieb den Verzicht auf jegliche Harmonik schließlich in den zwanziger Jahren des letzten Jahrhunderts der österreichische Komponist Arnold Schönberg mit seinem Zwölftonsystem.
Heute steht die Musik, wie alles andere auch, unter dem Einfluss der Denkweise des 20. Jahrhunderts wie Prinz Charles in seinem Buch „Harmonie“ so klar ausdrückt. Er schreibt: „Die Moderne durchdringt die Musik ebenso wie alles Übrige. Es ist vielleicht kein Zufall, dass gerade, als die Ideologie der Moderne im 20. Jahrhundert die traditionelle Auffassung von Kunst und Architektur zu verdrängen begann, Komponisten wie Schönberg und seine Neue Wiener Schule in ihrer Musik die Idee verfolgten, mit der traditionellen Harmonie der Töne zu brechen und stattdessen eine »atonale« Musikstruktur zu begründen – das heißt, ein Tonsystem, das nicht mehr auf einen festen Grundton oder eine bestimmte Tonart fixiert ist. Viele Musiker folgten ihrem Beispiel und komponierten sehr interessante, bewegende Musikwerke, aber ihr Schaffen führte zwangsläufig zu immer extremeren Experimenten, besonders in den 1960er und 1970er Jahren. Komponisten wie Stockhausen und die Darmstädter Schule zum Beispiel erzeugten Musik, die so unmelodisch ist, dass sie das Auffassungsvermögen überfordert und für die Mehrheit der Zuhörer völlig unverständlich ist. Wie ein Großteil der modernen Architektur jener Zeit ist sie zu »rational«, das heißt, sie wendet sich oft nur an den Kopf und in den meisten Fällen nur an die klügsten Köpfe, und so steckt in jeder dissonanten Wendung die implizite Botschaft, dass wir sie nur verstehen können, wenn wir genauso intelligent sind wie der Komponist. Das ist eine Vorstellung, die in krassem Widerspruch zum traditionellen Harmonieverständnis und seinem Grundakkord steht, nach dem wir Musik nicht »denken«, sondern sie fühlen und mit ihr mitschwingen wollen.“
Die Moderne Kunst ist ein Politikum. Alle staatlichen Auszeichnungen, Beihilfen und Preise für die Künstler, sind politisch gerichtet. Nur der wird hochgejubelt der besonders modern ist. Siehe zum Beispiel Joseph Beuys. Alle Menschen sollen von der Tradition von dem geraden Weg von dem Göttlichen in der Kunst getrennt werden. Die Moderne zerstört den Halt an Hergebrachtes, sie macht die Wähler gefügig für alle politischen Übertretungen der Mächtigen. Jemand, der keinen geraden Weg geht, keinen dicken Nacken hat, keine eigene Meinung vertritt, kein genaues Ziel kennt, der ist eben ohne Ziel.
Wer vom Ziel nichts weiß, der vom Weg nichts kennt.
Manche Meinungsbildner sagen doch immer, die Musik und gestaltende Kunst sei einfach ein Ausdruck der Zeit? – Ja, sicher, die Zeit ist nicht sauber, auch nicht schön; die Kunst ist auch nicht schön. Aber es hat auch den 30-jährigen Krieg gegeben. Da war die Zeit bestimmt nicht schön, aber die Musik und Kunst waren schön.
Zusammenfassung
Harmonikale Musik hören oder selbst spielen ist ein Lebenselixier, ein Ohrenschmaus. Ob Pflanze, Tier oder Mensch brauchen dieses Elexier um grösser, stärker und weiser auf dieser Welt zu werden. Die großen Mathematiker, Physiker und Philosophen unserer Vorzeit wie Phytagoras, Platon, Thales, Fibonacci, Descartes, Kepler, Kayser oder Haase haben die göttlichen Strukturen herausgefunden, den Goldenen Schnitt, die Fibonacci Reihe, die Primzahlen, den quadratura circuli, die Eulerschen Zahl e und viele weitere, die unsere Welt zusammenhalten. Die Welt ist Klang. Alle Harmonikalen Musiken sind nach den göttlichen Gesetzen aufgebaut. Seit Äonen von Jahren haben wir diese Gesetze in uns, über uns, neben uns eingesogen, programmiert und gespeichert. Musikalische und mathematische Beispiele zeigen ganz deutlich wie Leben und göttliche Harmonie zusammenhängen. Jeder der sein Unterscheidungsvermögen, sein Abschätzen, sein Abwägen geschult und geübt hat, merkt sofort wem ein göttliches innewohnt und wo es künstlich, abstrakt, verführerisch oder teuflisch wird.
Darum ist es eine Lebensaufgabe, die Harmonien der Musik und Mathematik zu studieren, zu praktizieren um ein waches, erstrebenswertes und erfülltes Dasein zu fristen und Mutter Erde nicht auszubeuten und zu zerstören sondern in jeder Hinsicht zu schützen und zu fördern.
Nachfolgend die nach harmonischen, starken Themen und Melodien ausgesuchten ca. 500 Musikbeispiele die hervorragend den eben beschriebenen göttlichen, volltönenden Gesetzen folgend, komponiert sind.
|
Ort |
Komponist |
gelebt |
Stück |
Dur/ |
Verz. |
Bem. |
| 2 | Albinoni, Tomaso | 1671-1750 | Konzert/Sinfonie/Trompete Oboe | – | – | |
| CD-Li | Trompetenkonzert Adagio in D-Moll | D-Dur | Op. 2 Nr. 6 | |||
| 69 | Sonata für Streicher | C-Moll | Op. 2 Nr. 4 | |||
| 95 | Konzert für Violine | G-Dur | Op.10 Nr. 4 | BS | ||
| 100 | Konzert Oboe | C-Dur | ||||
| 43 | Albrechtsberger, Johann Georg | 1736-1809 | Quartett Fuge | C-Dur | ||
| CD-Li | Konzert | B-Dur | ||||
| 101 | Abel, Karl Friedrich | Sinfonie | S-Dur | Op. 8 Nr. 6 | ||
| 6, 83 | Bach, Johann Sebastian | 1685-1750 | Konzert für Violine | A-Moll | Nr. 1 | BWV |
| „ | E- Dur | Nr. 2 | ||||
| “ und Oboe | D-Moll | 1063 | ||||
| 6 | “ Cembalo | C-Moll | ||||
| 6 | “ Trompete | D-Moll | ||||
| 2 | Brandenburgische 1 bis 6 | |||||
| 103 | Sinfonie Flöte aus Kantate 209 Monza quese | M-Moll | 209, BWV | |||
| 37 | Sinfonie aus Kantate Wir danken Dir Gott | 29 | ||||
| 3 | Kantate, Choral | 140 | ||||
| Trio Sonate | D-Moll | Nr. 3 | 527 | |||
| G-Dur | Nr. 6 | 530 | ||||
| 11 | Pli Toccata und Fuge | D-Moll | 565 | |||
| Fantasie | G-Dur | 572 | ||||
| Pastorale | F-Dur | 590 | ||||
| 46 | Sonate | G-Moll | 1029 | |||
| 11, 64 | Ouvertüre | D-Dur | Nr. 3 | 1068 | ||
| 3 | Menuett aus Suite | Nr. 2 | ||||
| 4 | Arie die Post | |||||
| 7 | Fantasie und Fuge | C-Moll | ||||
| Präludium und Fuge | A-Moll | |||||
| 85 | “ für Cembalo | D-Moll | ||||
| 60 | Sonate für Flöte | E-Moll | ||||
| 104 | Konzert für Cembalo und Orchester | C-Dur | ||||
|
Ort |
Komponist |
gelebt |
Stück |
Dur/ |
Verz. |
Bem. |
| CD-Li | Orgel | BWV | ||||
| „ | Wachet auf ruft uns d. Stirn | 645 | ||||
| „ | Präludium und Fuge | A-Moll | 543 | |||
| „ | O Mensch bewein Dein Sünd | 622 | ||||
| „ | Fantasie und Fuge | G-Moll | 542 | |||
| „ | Schmück Dich o liebe Seele | 654 | ||||
| „ | Passacaglia | C-Moll | 582 | |||
| „ | Sonate I | E-Dur | 525 | |||
| „ | Sonate II | C-Moll | 526 | |||
| „ | Sonate III | D-Moll | 527 | |||
| „ | Sonate IV | E-Moll | 528 | |||
| „ | Sonate V | C-Dur | 529 | |||
| „ | Sonate VI | G-Dur | 530 | |||
| CD-H | Orgel Präludium | 552 | ||||
| „ | 542, 645, 639, 565, 549, 654, 529, 593, 653, 546 | |||||
| „ | Toccata und Fuge | D-Moll | 565 | |||
| „ | C-Dur | 564 | ||||
| „ | F-Dur | 540, 538 | ||||
| 89 | Bach, Carl Philip Emanuel | 1714-1788 | Sinfonie Bach Werke V. | S-Dur | Nr. 2 | |
| 33 | Sinfonie | F- Dur | Nr. 3 | BS | ||
| 37 | D-Dur | |||||
| 48 | E-Moll | |||||
| 89 | D-Dur | 1008/131 | ||||
| 93 | Concerto für Oboe | S-Dur | ||||
| 80 | Trio für Laute | H-Moll | ||||
| Traverso Violine | ||||||
| Wortkann Verzeichnis | 143 | |||||
| 98 | Konzert | F-Dur | ||||
| Bach, Johann Christoph Friedrich | 1732-1795 | Sinfonie | F-Dur | Op. 3 Nr. 5 | ||
| Bruder von Johann Christian | ||||||
|
Ort |
Komponist |
gelebt |
Stück |
Dur/ |
Verz. |
Bem. |
| 91 | Bach, Johann Christian | 1735-1782 | Konzert | F-Dur | Op. 13 Nr. 3 | |
| 30 | Konzert für Klavier und Streichorchester | S-Dur | Op.7 | |||
| 42 | Sinfonie | G-Moll | Op.6 Nr. 6 | |||
| 34 | Sinfonie | S-Dur | Op. 18 Nr. 1 | |||
| 36 | B-Dur | Op. 18 Nr. 2 | ||||
| 69 | D-Dur | Op. 18 Nr. 4 | ||||
| 97 | A-Dur | Op. 18 Nr. 6 | ||||
| 104 | S-Dur | Op. 3 Nr. 3 | ||||
| 85 | Sinfonietta | C-Dur | ||||
| 54, 68 | Sonate | D-Dur | Op. 5 Nr. 2 | |||
| 51 | Präludium und Fuge für Cembalo | C-Moll | ||||
| 69 | Ouvertüre zur Oper | |||||
| La clemenza die Sipione | ||||||
| CD-Li | Bach, Wilhelm Friedemann | 1710-1784 | Sinfonie | F-Dur | Falk BV 67 | |
| CD-Li | Barbirolli, John | 1899-1970 | Konzert nach Pargolesi | C-Moll | ||
| 9 | Beethoven, Ludwig van | 1770-1827 | Sinfonie | C-Dur | Op.21 Nr. 1 | |
| Eroico | Es Dur | Op. 55 Nr.3 | ||||
| 4 | C-Moll | Nr. 5 | ||||
| 6, Pl | Nr. 7 | |||||
| Klavierkonzert | C-Dur | Op. 15 Nr. 1 | ||||
| 20 | „ | B-Dur | Op. 19 Nr. 2 | |||
| 11 | „ | C-Moll | Nr. 3 | |||
| 8 | „ | G-Dur | Nr. 4, Nr. 5 | |||
| Quartett | D-Dur | Op.18, Nr. 3 | ||||
| „ | C-Moll | Op.18, Nr. 4 | ||||
| 102 | Klavier Frühlings Sonate | F-Dur | Op. 27 | |||
| „ | Es Dur | Op. 12 Nr. 3 | ||||
| „ | A-Moll | Op. 23, Nr. 4 | ||||
| 8, Pl | Patetique | C-Moll | Op. 13 Nr. 8 | |||
| Mondscheinsonate | Cis Moll | Op. 27 Nr.2 | ||||
|
Ort |
Komponist |
gelebt |
Stück |
Dur/ |
Verz. |
Bem. |
| 22 | Mondscheinsonate | Es Dur | Op. 21 Nr.3 | |||
| 22 | Appassionata | Op. 57, Nr. 23 | ||||
| 88, Pl | Konzert für Violine | D-Dur | Op. 61 | BS | ||
| 94 | Rondo für Klavier und Orchester | B-Dur | ||||
| 82 | Barsandini, Francesco | Sonate für Flöte | G-Moll | |||
| 5 | Bartok, Bela | 1881-1945 | Rumänische Tänze | |||
| 103 | Bassanti, Francesko | Concetto Grosso | D-Dur | Op.3, Nr. 10 | ||
| 89 | Bellini, Vincenzo | 1801-1835 | Konzert Streicher Oboe | S-Dur | ||
| CD- Li | Oboen Konzert | E-Dur | ||||
| 30 | Biber, Heinrich Ignatz Franz | 1644-1704 | Sonata für Violine und basso continue | F-Dur | Nr. 3 | |
| 82 | Bizet, George | Larisienne Suite aus Musika zum Schauspiel von Lenfens Dodet |
Nr. 1 | |||
| 48 | Boccherini, Luigi | 1743-1805 | Cello Konzert | D-Dur | Op. 34 | |
| Sonate | E-Moll | Op.50 Nr.3 | ||||
| Konzert | C- Dur | Nr.4 | ||||
| 50 | Konzert für Flöte und kleines Streichorchester | |||||
| weiter Cellokonzert | B- Dur | |||||
| 71 | Boely, Jean Francois | 1739-1814 | Konzert für Harfe | C-Dur | ||
| 42 | Bononcini, Giovanni Battista | 1670-1747 | Sinfonie für 2 Trompeten mit Moris Andree | Op. 3a | ||
| B15 | Bonpart | Rezitativ | F-Dur | |||
| 92 | Boyce, William | 1711-1779 | Sinfonie | C-Dur | Nr. 3 | |
| 68 | Sinfonie | F-Dur | Nr. 6 | |||
| weiter Sonate | D-Moll | Nr. 7 | ||||
|
Ort |
Komponist |
gelebt |
Stück |
Dur/ |
Verz. |
Bem. |
| B5 | Brahms, Johannes | 1833-1897 | Ungarische Tänze 1-7 | |||
| B 13 | Konzert Violine u. Orchester | D-Dur | ||||
| B 17 | Bruch, Max | 1838-1920 | Violinkonzert | |||
| B 19 | Konzert für Violine und Orchester | G Moll | Op. 26 Nr.1 | |||
| 104 | Romanze | Op. 42 | ||||
| CD-Li | Buxtehude, Dietrich | 1637-1707 | Orgel Präludium | G-Moll | ||
| Bux 149, 223, 146, 197, 139, 211, 137, 183, 140, 199, 142, 178 |
||||||
| Bux 145, 153, 174, 161, 160, 154, 171, 203, 182, 155, 218, 156, 207 |
||||||
| 104 | Cannabich, Christian II/304 | Sinfonia Concertante für Flöte | C- Dur | |||
| 82 | Chavriet, Emanuel | Havanera | ||||
| 38 | Cherubini, Luigi | 1760-1842 | Sinfonie | D- Dur | ||
| Chopin, Frederic | 1810-1849 | Klavierkonzert | E-Moll | Op. 11, Nr. 1 | ||
| Polonaise | Cis-Moll | Op. 261, Nr. 1 | ||||
| 32/71 | Cimarosa, Domenico | 1749-1801 | Sinfonie für Flöte | G-Dur | ||
| CD-Li | Oboen Konzert | C-Dur | ||||
| 82 | Clementi, Muzio | Sinfonie | B-Dur | Op. 18 | ||
| 84 | Couperin, Amanliu | Suite aus dem 1. Buch de piece ceapsaint | B-Dur | |||
| B-Moll | ||||||
| 67 | Couperin, Francois | 1668-1733 | Imperiale für 2 Violinen | |||
| 88 | Corelli, Arcangelo | 1653-1713 | Concerto Grosso | D-Dur | Op.6, Nr.1 | |
| 52 | Concerto Grosso | B- Dur | Op. 6, Nr. 1 | |||
| 25/99 | Concerto Grosso, Weihnachtskonzet | G-Moll | Op. 6, Nr.8 | |||
| 35/44 | Concerto Grosso | S- Dur | Op. 6, Nr. 12 | |||
| 31/56 | Sarabande für Streichorchester | |||||
| 62 | Concerto Grosso | F-Dur | Op.6, Nr. 6 | |||
| 63 | Trio Sonate | F-Dur | Op.2, Nr. 7 | |||
| 65 | Concerto Grosso | F-Dur | Nr.12 | |||
| 86 | Concert | D-Dur | Op.6, Nr.4 | |||
| 91 | Concerto Grosso | B-Dur | Op. 6, Nr.11 | |||
| CD-Li | Concerto | F-Moll | Nr. 8 | |||
| Opernkonzert | A- Dur | |||||
| 71 | Crussel, Bernhard Henrik | 1775-1838 | Sinfonia Concertante für Klarinette | B-Dur | Op. 3 | |
| B 10 | Csermack, Antal Gyorgy | 1774-1822 | Streichquartett | |||
| B7 | Dall Abaco, Evaristo Felice | 1675-1742 | Konzert | E-Dur | Op.6 Nr. 2 | |
| B13 | Konzert | H-Moll | Op.2 Nr. 8 | |||
| 58 | Konzert | F-Dur | Op. 6 Nr. 6 | |||
| 60 | Konzert | F-Dur | Op. 6 Nr. 3 | |||
| 81/2 | Konzert | E-Dur | Op. 6 Nr. 2 | |||
| 103 | Konzert Streicher | H- Moll | Op.2 Nr. 8 | |||
| 37 | Danzi, Franz | 1763-1826 | Flötenkonzert | G-Dur | Op. 30 Nr. 1 | |
| 55 | Quartett für Flöte | D-Dur | ||||
| 68 | Konzert | D-Moll | Nr. 2 | |||
| 72 | Sinfonie | G-Dur | ||||
| 63 | Dittersdorf, Karl Ditters von | 1739-1799 | Overtüre zu Lester Ossia | |||
| 31 | Donizetti, Gaetano | 1797-1848 | Sinfonie | D-Moll | ||
| 89 | Quartett | D-Dur | ||||
| 39/56 | Dusek, Frantisektauer | 1731-1799 | Schüler von Wagenseil und Mozart, Sinfonie | S-Dur | BS | |
| B16 | Dvorak, Antonin | 1841-1904 | Slavische Rhapsodie | |||
| 66 | Rhapsodie | A-Moll | Op. 14 | |||
| 66 | Endler, Johann Samuel | 1700-1762 | Overtüre | D-Dur | Nr. 7 | |
| 42 | Fasch, Johann Friedrich | 1688-1758 | Konzert für Oboe und Streicher | G-Dur | ||
| 95 | Konzert für Flöte | G-Dur | ||||
| 90 | Sonate, 2 Violinen | D-Moll | ||||
| 100 | Trompetenkonzert | D-Dur | ||||
| CD-Li | Konzert für Oboe und Streicher | D-Moll | ||||
| CD-Li | Fiorillo, Federigo | 1755-1823 | Sinfonia Concertante | F-Dur | ||
| 66 | Frank, Caspar | Konzert | H-Moll | Op. 11, Nr. 2 | ||
| B28 | Friedrich der Große | 1712-1786 | Flötenkonzert | C-Dur | ||
| 98 | Sinfonie | G-Dur | Nr. 1 | |||
| 67 | Froberger, Johann Jacob | 1616-1667 | Suite für Cembalo | A-Dur | Nr. 15 | |
| weitere Capriccio | Nr. 13 | |||||
| Fantasia | Nr. 17 | |||||
| Toccata | Nr. 2 | |||||
| Concert | Nr. 11 | |||||
| Ricercare | Nr. 11 | |||||
| 105 | Gassmann, Florian | Quartett | D-Moll | Nr. 3 | ||
| 90/B15 | Geminiani, Francesco | 1680-1762 | Concerto Grosso Violine | G-Moll | Nr. 12 | BS |
| 71 | A-Dur | Nr. 9 | ||||
| nach Corellis la folie 3/4 | Op. 5 | |||||
| 56 | Golabeck, Jacob | Sinfonie | C-Dur | |||
| 93 | Graun, Michael Gottlieb | Overtüre | D-Moll | |||
| 101 | Graun, Johann Gottlieb | Konzert für Violine | C-Moll | |||
| 31/45 | Gretriy, Andre Ernest Modest | 1741-1813 | Sinfonie | G-Dur | Op. 3 Nr. 1 | |
| 45/31 | Sinfonie | G-Dur | Op. 3 | BS | ||
| B14 | Gyrwetz | Symphonie | Es Dur | Op. 8 | ||
| 102 | Händel, Georg Friedrich | 1685-1759 | Wassermusik Suite Feuerwerksmusik | G-Dur | Nr. 3 | |
| 7,82 | Overtüre zu Ottone | |||||
| 74 | Overtüre zu Alexanderfest | |||||
| 40 | Orgelkonzert | G-Moll | Op. 4 Nr. 4 | |||
| 3 | Orgelkonzert | G-Moll | Op. 4 Nr. 9,10,11,12 | |||
| 91 | Konzert Orgel und Trompete | D-Dur | ||||
| 3 | Hornkonzert | |||||
| 28, 33 | Oboen Konzert | B-Dur | Nr. 1 | |||
| Oboen Konzert | B-Dur | Nr. 2 | ||||
| Oboen Konzert | G-Moll | Nr. 3 | ||||
| 82 | Konzert | F-Dur | Op. 6, Nr. 9 | |||
| 97 | Doppelkonzert für Horn | F-Dur | Nr. 3 | |||
| 81,52 | Concerto Grosso Flöte | B-Dur | Op. 3 Nr. 1 | |||
| 15,44 | B-Dur | Op. 3, Nr.2 | ||||
| 59,64 | B-Dur | Op. 3, Nr.2 | ||||
| 88 | F-Dur | Op. 3, Nr. 4 | ||||
| 45 | D-Moll | Op. 3, Nr. 5 | ||||
| 87 | D-Dur | Op. 3 Nr. 6 | ||||
| 63 | E-Moll | Op. 6, Nr. 3 | ||||
| 33 | G-Moll | Op. 6, Nr. 6 | ||||
| 34 | Op. 6, Nr. 10 | |||||
| 77 | A-Dur | Op. 6, Nr. 11 | ||||
| 80 | Horn | S-Dur | ||||
| CD-Li | Concerti Grossi | Op.6, Nr. 1 und 2 | ||||
| Feuerwerksmusik | ||||||
| Concerti Grossi | Op.6, Nr. 3,9,10,11,12 | |||||
| Larghetto from serse Trompetenkonzert | B-Dur | |||||
| Larghetto from serse Trompetenkonzert | D-Dur | |||||
| 69 | Haydn, Joseph | B-Dur | ||||
| PL,23,3 | für Trompete | S-Dur | ||||
| 73 | für Flöte | F-Dur | ||||
| ? | Streichquartette Lerchen Quartett | D-Dur | Op. 64, Nr.5 | |||
| 16 | Reiterquartett | G-Moll | Op.74, Nr. 3 | |||
| CD-Li | Konzert | D-Dur | ||||
| PL | Divertimenti für Flöte und Streicher | |||||
| 16,55 | Für Cembalo und Violine | F-Dur | ||||
| 70 | für Horn | D-Dur | ||||
| 37 | Eine Macht eine Dienerin Maria | |||||
| 87 | Berenitsche kefay Cantate | |||||
| CD-Li | Hornkonzert | D-Dur | Nr. 1 | |||
| Symphonie | G-Dur | Nr. 94 | ||||
| D-Dur | Nr. 104 | |||||
| Hornkonzert | E-Dur | |||||
| B3 | Hamal, Henri | 1744-1820 | Largoaus Konzert | D-Dur | ||
| Hasse, Johann Adolf | 1699-1783 | Orgelkonzert, Concerto | F-Dur | Nr. 1, 5 | ||
| G-Dur | Nr. 3 | |||||
| 6 | Helmich, Johann Christian | 1694-1758 | ||||
| 70 | Roman Orchester Suite aus Drating Helms Musiquen |
|||||
| B3 | Hertel, J.W. | 1727-1789 | Konzert Larghetto | Es Dur | ||
| 82 | Haydn, Joseph | 1732-1809 | Sinfonien | F-Dur | Nr. 5 | Prager Verz. |
| 46/88 | le Matin | D-Dur | Nr.6 | |||
| 57 | le midi | C-Dur | Nr.7 | |||
| 16 | Nr. 8 | |||||
| 10 | La Passion | Es-Dur | Nr.9 | |||
| 53 | B-Dur | Nr.35 | ||||
| 60 | C-Dur | Nr.38 | ||||
| 40/74 | S-Dur | Nr.43 | ||||
| 86 | F-Moll | Nr.49 | ||||
| 15 | G-Dur | Nr.88 | ||||
| 16 | Imperiale | D-Dur | Nr.53 | |||
| 84 | D-Dur | Nr.57 | ||||
| 65 | D-Dur | Nr.61 | ||||
| 47 | F-Dur | Nr.67 | ||||
| 50 | B-Dur | Nr.68 | ||||
| 33 | Nr.84 | |||||
| 65 | B-Dur | Nr.85 | ||||
| 7,32 | D-Dur | |||||
| 15 | G-Dur | Nr. 89 | ||||
| 95, B8 | mit Paukenschlag | B-Dur | Nr. 98 | |||
| 62 | Paukenwirbel | S-Dur | Nr.103 | |||
| Pl | Die Uhr | D-Dur | Nr. 101 | |||
| Pl | London | D-Dur | Nr. 104 | |||
| Pl | B-Dur | Op.84 | ||||
| 1 | Schulmeister | S-Dur | ||||
| 105 | Sonate für Klavier | G-Dur | RBV IV/6 | |||
| 102 | Trio für Flöte | G-Dur | RBV 47 | |||
| 72 | Trio für Flöte | D-Dur | 4 Nr.11 | DBV | ||
| 96 | Adagio Klavier | F-Dur | 17 Nr. 9 | |||
| Pl, 70 | Konzerte für Cello | D-Dur | Op.101, Nr. 1 | |||
| 45 | für Cello | C-Dur | Nr.7 | B1 | ||
| 34 | für Violine | G-Dur | ||||
| 61 | für Violine | C-Dur | ||||
| 56 | für Cembalo | D-Dur | BS | |||
| 56 | für Oboe | C-Dur | ||||
| 81 | Haydn, Michael | 1737-1806 | Sinfonien | A-Dur | PVZ 33 | |
| 53/93 | D-Dur | PVZ 42, BS | ||||
| 77 | D-Dur | 52 | ||||
| 78 | G-Dur | |||||
| 53 | ach Konzert von J.Ch. Bach | G-Dur | ||||
| 81 | Konzert für Violine | B-Dur | ||||
| 3 | Konzert Allegro | D-Dur | ||||
| 54 | Hoffmeister, Franz Anton | 1754-1812 | Musikalienhändler, seichte, leichte Musik, Quartett für Flöte |
A-Dur | ||
| B3 | Hummel, Johann Nepomuk | 1778-1837 | Konzert nur Andante | Es – Dur | ||
| B23 S | Konzert für Trompete und Orchester, C.D. Reinhart Trompete |
Es – Dur | ||||
| Münchner Philharmonie | ||||||
| 38 | Konzert für Fagott und Orchester | |||||
| 48 | Konzert für Mandoline | B-Dur | ||||
| CD-Li | Trompetenkonzert | E-Dur | ||||
| 52 | Kiel, Friedrich August | 1821-1885 | Konzert für Flöte | G- Dur | ||
| 52/81 | Kramar, Frantisek Vincence | 1759-1831 | Sinfonia | D-Dur | ||
| 64 | Kraus, Joseph Martin | 1756-1792 | Sinfonie | D-Dur | ||
| 80 | Sinfonie | C-Moll | ||||
| weitere Violin Konzert | C-Dur | |||||
| 37 | Krebs, Johann Ludwig | 1713-1780 | Gitarrenkonzert | G-Dur | ||
| 82 | (Schüler von J.S. Bach) | Sonate für Flöte | G-Dur | |||
| B10 | Leclair, Jean Marie | 1697-1764 | Konzert | G-Moll | ||
| B28 | Konzert für Oboe und Streicher | C-Dur | Op. 7.3 | |||
| 31 | Konzert für Violine und Orchester | D-Moll | ||||
| 37/28 | Konzert Violine | C-Dur | Op. 73 | BS | ||
| 87 | Konzert | C-Dur | Op. 3 | |||
| Liszt, Franz v. | 1811-1886 | Ungarische Rhapsodie 2,5,6,12,15 | ||||
| Ungarische Rhapsodie 1,2,3 und 6 | ||||||
| 78 | Locatelli, Pietro – Antonio | 1695-1764 | Introduktion Theatrale | D-Dur | Op. 4, Nr.1 | |
| 15 | Concerto Grosso für 4 Violinen | F-Dur | Op. 7, Nr.12 | |||
| 85 | Concerto Grosso | C-Moll | Op. 1, Nr. 11 | |||
| 96 | Concerto Grosso | G-Moll | Op.1, Nr. 12 | |||
| CD-Li | Concerto Grosso | Op.3, Nr. 2 | ||||
| 46 | Loeillet, Jean-Babtiste | 1680-1730 | Sonate | G-Dur | ||
| 47 | Ouvertüre und Suite, Comedy | |||||
| Ballais de Burguis Gentillhorn | ||||||
| B28 | Marcello, Alessandro | Konzert für Oboe und Streicher | D-Moll | |||
| CD-Li | Marcello, Benedetto | 1686-1739 | Oboen Konzert | D-Moll | ||
| Sonate | Op.2, Nr. 11 | |||||
| Köchelverz. | ||||||
| 105 | Mozart, Wolfgang Amadeus | 1756-1791 | Sinfonie | B-Dur | Nr. 5 | K.V. 22 |
| 68 | Konzert | G-Dur | Nr. 4 | 41 | ||
| 66,44 | Sinfonie | F-Dur | 43 | |||
| 54 | C-Dur | 73 | ||||
| 74 | G-Dur | 74 | ||||
| 73 | F-Dur | 75 | ||||
| 43 | G-Dur | 81 | ||||
| 62 | G-Dur | 110 | ||||
| Sinfonie | F-Dur | Nr. 13 | 112 | |||
| 52 | Konzert | A-Dur | Nr. 14 | 114 | ||
| 36 | Sinfonie | B-Dur | BS | 119 | ||
| 58 | Divertimento | F-Dur | Nr. 3 | 138 | ||
| 92 | Konzert | D-Dur | 175 | |||
| 87 | Sinfonie | A-Dur | 201 | |||
| 72 | Violinkonzert | Nr. 1 | 207 | |||
| Nr. 2 | 211 | |||||
| G-Dur | Nr. 3 | 216 | ||||
| D-Dur | Nr. 4 | 218 | ||||
| A-Dur | Nr. 5 | 219 | ||||
| 6 | Konzert Lützow | C-Dur | 246 | |||
| 85 | Divertimento | F-Dur | 247 | |||
| Haffner Serenade | Es Dur | 250 | ||||
| Kontratanz | 101,267 | |||||
| Klavierkonzert | Es Dur | 271 | ||||
| 36 | Flötenkonzert | C-Dur | 299 | |||
| 70 | Sonate für Klavier | G-Dur | 301 | |||
| 10 | Flötenkonzert | G-Dur | 1 | 313 | ||
| D-Dur | 2 | 314 | ||||
| 34 | Konzert Rondo | D-Dur | 328 | |||
| Klaviersonate | A-Dur | 331 | ||||
| 77 | Divertimento Salzburger Sinfonie 2 | B-Dur | 337 | |||
| 37 | Märsche | D-Dur | 335 | |||
| 21 | Konzertante Sinfonie Oboe Violine | 364 | ||||
| 65 | Konzert für Horn | S-Dur | 371 | |||
| 62 | Rondo | C-Dur | 373 | |||
| 91 | Sonate für Klavier und Flöte | B-Dur | 378 | |||
| Sinfonie Haffner | D-Dur | Nr. 35 | 385 | |||
| 86 | Konzert Rondo | 386 | ||||
| 92 | Fantasie für Klavier | D-Moll | 399 | |||
| 39,64 | Sinfonie | C-Dur | Nr. 36 | 425 | ||
| 59 | C-Dur | Nr. 36 | 426 | |||
| 1 | Messe | C-Moll | 427 | |||
| Streichquartett, Jagdquartett | B-Dur | 458 | ||||
| 31 | Klavierkonzert | D-Dur | 459 | |||
| Klavierkonzert | D-Moll | 466 | ||||
| Klavierkonzert | A-Dur | 488 | ||||
| 25,78 | Klavierkonzert | C-Dur | Nr. 25 | 503 | ||
| 11 | Sinfonie Prager S | D-Dur | 504 | |||
| 14 | Eine kleine Nachtmusik | G-Dur | 525 | |||
| 63 | Sechs deutsche Tänze | 536 | ||||
| 6 | Krönungskonzert | D-Dur | 537 | |||
| 12 | Sinfonie Jupiter | C-Dur | Nr. 41 | 551 | ||
| 25,86 | Klavierkonzert | B-Dur | Nr. 27 | 595 | ||
| 69 | Konzert für Klarinette | A-Dur | 622 | |||
| 16 | Linzer Sinfonie | |||||
| 16 | Hornkonzert | S-Dur | ||||
| 35 | Overtüre und Ballett zur Oper Idomeo | |||||
| 53 | Sinfonie | D-Dur | ||||
| 59 | Sinfonie Neue Lambacher | G-Dur | ||||
| CD-H | Hornkonzert | Es Dur | Nr. 3 | 447 | ||
| Hornkonzert | D-Dur | Nr. 1 | 412 | |||
| Oboen Konzert | C-Dur | 314 | ||||
| Sonate | A- Moll | 310 | ||||
| Sonate | A-Dur | 331 | ||||
| Sonate | C-Dur | 545 | ||||
| Sonate | D-Dur | 576 | ||||
| Menuett | D-Dur | 355 | ||||
| Overtüre Figaros Hochzeit | 492 | |||||
| Klaviersonate | C-Dur | Nr. 15 | C 545 | |||
| Serenade | G-Dur | Nr. 13 | K 525 | |||
| Serenade Nottur | D-Dur | D 239 | ||||
| Klaviersonate | G-Dur | Nr. 5 | G 283 | |||
| Klavierkonzert | D-Dur | Nr. 26 | D 537 | |||
| Klarinettenquintett | A-Dur | A 581 | ||||
| Hornkonzert | Es Dur | Nr. 4 | E 495 | |||
| Klavierkonzert | C-Moll | Nr. 24 | K 491 | |||
| Klavierkonzert | E-Dur | Nr. 9 | K 271 | |||
| Klavierkonzert | G-Dur | Nr. 17 | 453 | |||
| Orchesterkonzert | D-Dur | 191 | ||||
| Konzertante Sinfonie | E-Dur | 297 b | ||||
| Konzert | E-Dur | Nr. 21 | 467 | |||
| Lodron Nachtmusik | Nr. 1 | 247 | ||||
| CD-Li | Symphonie Prager | Nr. 38, 40 | ||||
| Prager | D-Dur | 504 | ||||
| G-Moll | Nr. 40 | 550 | ||||
| Symphonie | G-Moll | Nr. 25 | 183 | |||
| Konzert für Fagott | B-Dur | 191 | ||||
| Konzert für Violine | D-Dur | Nr. 4 | 218 | |||
| Symphonie Haffner | D-Dur | Nr. 35 | 385 | |||
| Linz | C-Dur | Nr. 36 | 425 | |||
| Prager | D-Dur | Nr. 38 | 504 | |||
| E-Dur | Nr. 39 | 543 | ||||
| G-Moll | Nr. 40 | 550 | ||||
| Jupiter | C-Dur | Nr. 41 | 551 | |||
| Oboen Konzert | C-Dur | 285 D | ||||
| Phantasia | C-Moll | 475 | ||||
| Sonate | C-Moll | 457 | ||||
| Thema | F-Dur | 54 | ||||
| Menuett | F-Dur | 2 | ||||
| Klavierstück | B-Dur | 15 | ||||
| Sonate | G-Dur | 283 | ||||
| Mozart, Leopold | 1719-1787 | Vater von W.A. Mozart | ||||
| B23 S | Konzert Solotrompete, 2 Hörner, Frau C, D.Reinhart, Münchner Phil. |
D-Dur | ||||
| 30 | Sinfonie | G-Dur | ||||
| 44 | Divertimento | B-Dur | BS | |||
| 46 | Divertimento | D-Dur | ||||
| CD-Li | Konzert Sinfonia da Caccia für 4 Hörner | G-Dur | ||||
| 84 | Mareau, Marin | Le foliet de e´spanie für Flöte | ||||
| B3 | Martini, G.B. | 1706-1784 | Toccata | |||
| 80 | Matteis, Nicola | 17. Jahrh. | Suite in E für Violine und Basso Kontinuo, aus The Kingston Musik |
|||
| 39 | Mao, Anton | Sinfonia | C-Moll | Nr. 4 | ||
| CD-H | Mendelssohn Bartholdy, Felix | 1809-1847 | Violinkonzert | E-Moll | Op. 64 | |
| 30 | Jugendsinfonie | D-Dur | Nr. 2 | |||
| 47 | Jugendsinfonie | Nr. 9 | ||||
| Pl | Die Italienische | A-Dur | Op.90, Nr. 4 | |||
| Pl,1,19 | Konzert für Violine | E-Moll | Op. 64 | BS | ||
| 9 | Sonate für Cello, Klavier | D-Dur | ||||
| 14 | Oktett für Violine | E-Dur | Op.100 | |||
| 34 | Mercadante, Saverio | 1795-1870 | Sinfonie über Sabbat Marta von Rossini | |||
| 78 | Konzert für Flöte und Orchester | D-Dur | ||||
| 61 | Mirjewski, Adam | Zwei Cancomen | ||||
| B 27 | Molter | 1695-1765 | Konzert Azur, Klarinette | |||
| 57 | Monn, Mathias G. | 1717-1750 | Konzert | B-Dur | ||
| weiter Cello Konzert | G-Moll | |||||
| 103 | Sinfonia | H-Dur | ||||
| 38 | Muffat, Georg | 1653-1704 | Sonata | E-Moll | Nr. 4 | |
| 59 | Concerto Grosso | A-Dur | Nr. 2 | |||
| 77 | Neefe, Christian Gottlob | 1784-1798 | Variationen aus dem Priestermarsch der Zauberflöte |
|||
| CD-Li | Pachelbel | Canon Gigue | ||||
| Paganini, Niccolo | 1782-1840 | Violinkonzert | D-Dur | Op. 6, Nr. 1 | ||
| B3 | Violinkonzert | H-Moll | Op. 7, Nr. 2 | |||
| B 21 | La Camanella für Violine und Orchester | |||||
| B21 | L Prima Vera (Frühling) Sonate für Violine und Orchester |
A-Dur | ||||
| B 23 S | Für Violine und Orchester | A-Moll | Nr. 5 | |||
| Ma estosa Sonata sentimentale Salvatore Accardo Violine London Phil. |
||||||
| Hymne Joseph Haydns, Gott erhalte Franz der Kaiser |
||||||
| Pisendel, Johann Georg | 1687-1755 | Konzert Violine, Streicher, Bass, Konzert in D | Es -Dur | |||
| B 4 | Purcell, Henry | 1659-1695 | Trompet Voluntry | |||
| 40 | Suite für Orchester The guardian Nut | |||||
| 50 | Suiten aus „The married beau“ | |||||
| 95 | Sonate für Streicher | D-Dur | ||||
| B 28 | Quantz, Johann Joachim | 1697-1773 | Flötenkonzert | G-Dur | ||
| 63 | Flötenkonzert | E-Moll | ||||
| 83 | Konzert für Flöte und Streicher | G-Dur | ||||
| CD-Li | Rignini, Vincenzo | 1756-1812 | Oboen Konzert | C-Dur | ||
| 46/83 | Rossini, Gioacchino | 1792-1868 | Sonata a Quattro | G-Dur | Nr. 1 | |
| A-Dur | Nr. 2 | BS | ||||
| 97 | C-Dur | Nr. 3 | ||||
| 50/58 | Introduktionen für Klarinette | C-Dur | ||||
| 68 | Sonata a Quattro | S-Dur | Nr. 5 | |||
| 73 | Serenade | S-Dur | ||||
| 73 | Sonata | G-Dur | Nr. 1 | |||
| 73 | Quartett für Flöte aus der Overtüre zum Barbier von Sevilla |
F-Dur | ||||
| Serenata per piclo complesso | S-Dur | |||||
| Sonata a Quattro für 2 Violinen | G-Dur | Nr. 1 | ||||
| 82 | Rossi, Michelangelo | Toccata für Cembalo D-Moll | ||||
| 102 | Rosemüller, Johann | Sonate | C-Dur | Nr. 4 | ||
| B 27 | Rolla, Alessandro | 1757-1841 | Konzert für Basset Horn | F-Dur | ||
| 60 | Rohmann, Johann Helmich | Sonate für Flöte | D-Dur | |||
| 104 | Robischeck, Jean Hugo | Quasi una Phantasia für Klavier | B-Moll | Op. 20 | ||
| B 15 | Riciotti | Concertino | G-Dur | Nr. 1 | ||
| 77 | Rejcha, Antonin | 1770-1836 | Quintett | S-Dur | Op. 88 Nr. 2 | |
| 96 | Reichardt, Johann Friedrich | Konzert Hammer Klavier | G-Moll | |||
| 104 | Reicha, Antoine | Trio für Horn | E-Moll | Op. 83 | ||
| 80 | Rameau, Jean Philippe | 1683-1764 | Suite Poera Ballet L’Enfant gallant | Nr. 1 | ||
| 60 | Saint Piece de Passand | |||||
| 90 | Konzert | Nr.3 | ||||
| B 5 | Rachmaninow, Sergey | 1873-1943 | Klavierkonzert | C-Moll | Nr. 2 | |
| 94 | Salieri, Antonio | Konzert Violine Oboe | D-Dur | Nr. 3 | ||
| 32 | Samartini, Jovanni Batista | 1700-1775 | Sinfonie | G-Dur | ||
| 83 | Samartini, Joseppe | Konzert | G-Moll | Nr. 8 | ||
| 88 | Konzert für Viola | C-Dur | ||||
| 63 | Scarlatti, Alessandro | 1660-1725 | Patita | D-Moll | ||
| 80 | Sonate Paul Patrik Verzeichnis | F-Dur | PP 162 | |||
| 80 | Sonate | C-Dur | PP 132 | |||
| 90 | Quartettino Blockflöte, Oboe | F-Dur | ||||
| 90 | Scarlatti, Dominico | 1685-1757 | Concerto Grosso | A-Dur | Nr. 1 | BS |
| 65 | Concerto Grosso | D-Moll | Nr. 3 | |||
| 87 | Concerto Grosso | D-Dur | Nr. 6 | |||
| 91 | Concerto Grosso | E-Moll | Nr. 8 | |||
| 90 | Sonate | B-Dur | P.V. 529 | |||
| B 5 | Saint Saens, Camille | 1835-1921 | Konzert für Harfe und Orchester | G-Dur | Op. 159 | |
| B12/92 | Introduktion und Rondo pricioso violine | Op. 28 | ||||
| B 12 | Havanaise Kubanischer Tanz | Op. 83 | ||||
| B 17 | Karneval der Tiere | |||||
| 68 | Introduktion und Rondo | |||||
| 57 | Schaffrath, Christoff | 1709-1763 | Konzert | A-Moll | ||
| 18 | Schubert, Franz | 1797-1828 | Sinfonie | D-Dur | Nr.1 | |
| 18 | Tragische Sinfonie | C-Moll | Nr. 4 | |||
| 61, 18 | Sinfonie | B-Dur | Nr. 5 | BS 485 | ||
| Unvollendete Sinfonie | H-Moll | Nr. 8 | ||||
| C-Dur | Nr. 9 | |||||
| Klaviersonate | A-Dur | BS 959 | ||||
| 58 | Overtüre | D-Dur | Nr. 1 | BS 590 | ||
| 70 | Divertimento | Po. 84 Nr. 2 | BS 823 | |||
| 34,51,61 | Violinkonzert | D-Dur | BS 345 | |||
| 75, 88 | ||||||
| CD-Li | Symphonie 5 D + 85 u. 8 D Unvollendete | 759 | ||||
| B2, 17 | Schumann, Robert | 1810-1856 | Frühlingssymphonie 3. Satz | |||
| Konzert für Traversflöte | ||||||
| Kinderszenen | Po. 15 | |||||
| B 21 | Klavierkonzert | A-Moll | Op. 54 | |||
| Cellokonzert | A-Moll | Op. 129 | ||||
| CD-Li | Klaviersonate | F-Moll | ||||
| Arabeske | C-Dur | Op. 18 | ||||
| Waldzenen | Op. 82 | |||||
| B 17 | Schwindel, Friedrich | Konzert für Traversflöte | D-Dur | |||
| 60 | Schwarzkopf, Theodor | Overtüre für Trompete | C-Dur | |||
| 60 | Stamitz, Carl | 1745-1801 | Sinfonia | D-Dur | Nr. 19 | |
| B 10 | Sinfonia concert ante für Violine, Viola, Orchester | D-Dur | ||||
| B 27 | Konzert für Klarinette | Es Dur | ||||
| 105 | Orchester Quartett | F-Dur | Op. 4, Nr. 4 | |||
| 38, 61 | Orchester Quartett für Violine | G-Dur | ||||
| 85, 64 | Konzert für Flöte | G-Dur | Op. 29 | |||
| 100 | Konzert Klarinette | B-Dur | ||||
| 64 | Flötenkonzert | G-Dur | Op. 29 | |||
| 92 | Stamitz, Johann Anton Wenzel | Konzert für Flöte | C-Dur | |||
| 103 | Starzer, Josef | Divertimento | C-Dur | |||
| 72 | Stradella, Alessandro | 1644-1682 | Sonate für Trompete | D-Dur | ||
| CD-Li | Sinfonie zu drei für Streicher und Cembalo | D-Dur | ||||
| B3 | Strauss, Richard | 1864-1949 | Hornkonzert Csárdás aus Ritter Pasman | S-Dur | ||
| 104 | Rosen aus dem Süden | |||||
| 55 | Strauss, Johann (Vater) | 1804-1849 | Rosen aus dem Süden Walzer, | |||
| Rosenkavalier Ausschnitt 1. u. 2. Akt | ||||||
| Walzer Spährenklänge | Op. 235 | |||||
| B 14 | Tapray | Konzert Sinfonie Cembalo Klavier | Op. 9 | |||
| 97 | Tartini, Giuseppe | Konzert Cello | A-Dur | |||
| 51, 85 | Telemann, Georg Philip | 1681-1767 | Trio aus 1. Teil Tafelmusik | S-Dur | ||
| 42 | Overtüre 3. Teil Tafelmusik | |||||
| 44 | Violinkonzert | G-Dur | ||||
| 44 | Sinfonie | F-Dur | Nr. 6 | |||
| 59, 100 | Konzert für Trompete | D-Dur | ||||
| 80 | Konzert für Flöte | E-Moll | ||||
| Konzert Violine und Orchester | D-Dur | |||||
| 93 | Konzert | B-Dur | ||||
| 58 | Overtüre | G-Dur | ||||
| 13, 3 | Overtüre | F-Dur | ||||
| 41 | Overtüre | D-Dur | ||||
| B 4 | Trompetenkonzert | D-Dur | ||||
| 63 | Overtüre La Changement | G-Moll | ||||
| B 3 | Tempo Justo aus Sonate | G-Moll | ||||
| 40 | Flötenkonzert | A-Moll | ||||
| 33 | Flötenkonzert | E-Dur | ||||
| 36 | Flötenkonzert | D-Dur | ||||
| CD-Li | Konzert D-Dur 3 Corti und Streicher | D-Dur | ||||
| Drei Darmstatt Ouvertüren | C-Dur | |||||
| Suite | A-Moll | |||||
| Viola Concert | G-Dur | |||||
| Quartett Tafelmusik 1 | D-Dur | |||||
| Sonate 2 Flöten | B-Moll | Op. 2, Nr.5 | ||||
| Overtüre Darmstadt | D-Dur | |||||
| Trompetenkonzert | D-Dur | |||||
| Suite La Changeante | ||||||
| Tafelmusik 2 | D-Dur | |||||
| Trompetenkonzert | E-Moll | |||||
| Hornkonzert für 3 Hörner | D-Dur | |||||
| 44 | Violinkonzert | G-Dur | ||||
| Sinfonie | F-Dur | Nr. 6 | ||||
| 59 | Konzert für Trompete | D-Dur | ||||
| 80 | Konzert für Flöte | E-Moll | ||||
| 95 | Konzert für Oboe | F-Moll | ||||
| CD-Li | Konzert Violine, Oboe, Horn | F-Dur | ||||
| Konzert Blockflöte, Fagott, Streicher | F-Dur | |||||
| Hronkonzert | D-Moll | |||||
| 97 | Torelli, Giuseppe | 1658-1709 | Sonate | A-Moll | ||
| CD-Li | Sonate zu 5 Konzert für Trompete | D-Dur | Nr.1 | |||
| 57 | Thoma, Mathias | Partita | A-Dur | |||
| Tschaikowsky, Peter | 1840-1893 | Serenade Streichorchester | C-Dur | Op. 48 | ||
| 102 | Tscherny, Karl | Rondino sur en motive de Heyden für Klavier | Op. 99 | |||
| 31 | Verschragen, Gabriele | Drei flämische Tänze | ||||
| 41,CD-H | Vieuxtemps, Henri | 1820-1881 | Violinkonzert Gretry | A-Moll | Op. 37, Nr.5 | |
| 67 | Vivaldi, Antonio | 1678-1741 | Konzert für Violine aus den Vierjahreszeiten | F-Moll | Op. 8, Nr. 4 | |
| 24 | 4 Jahreszeiten | Op. 8, 1-4 | PV 241, 336, | |||
| 257, 442 | ||||||
| Konzert für 2 Violinen und Laute | D-Dur | 93 | ||||
| 48 | Konzert Die Nacht | B-Dur | Nr. 1 | |||
| 74 | La notte | G-Moll | Op.. 10, Nr. 2 | |||
| 84 | A-Dur | |||||
| 84, 100 | Trio für Flöte | A-Moll | ||||
| 12 | Concerto Grosso | H-Moll | Op. 3, Nr. 10 | |||
| 15 | Concerto Grosso | F-Dur | ||||
| 13 | Concerto grosso viola da more | D-Dur | ||||
| 12, 86 | Concerto grosso viola da more | D-Moll | 103 | |||
| 12 | Concerto Grosso Horn und Streicher | F-Dur | ||||
| 12 | Concerto Grosso Flöte | F-Dur | ||||
| 12 | Concerto Grosso | A-Moll | Op. 3, Nr. 8 | |||
| 43 | Concerto Grosso | C-Moll | ||||
| 4 | Concerto Grosso Trompete | |||||
| 3 | Concerto Grosso Trompete Allegro | Nr. 3 | ||||
| Pl | L‘estro Armenico Concert Violine Cello | |||||
| 46 | Konzert Violine Gitarre | G-Moll | BS | |||
| 62 | Konzert Blockflöte | D-Dur | Op. 10, Nr. 3 | |||
| 89 | Konzert für Piccolo Flöte | C-Dur | BS | |||
| 90 | Konzert für Violine | G-Moll | Op. 12, Nr. 3 | |||
| 101 | Concerto in due Cori | BS | ||||
| 104 | Konzert 2 Blockflöten | D-Moll | ||||
| 105 | Sonate für Flöte und Laute | F-Dur | ||||
| 100 | Flötenkonzert | A-Moll | ||||
| CD-H | Vierjahreszeiten | |||||
| Frühling | E-Dur | 269 | ||||
| Sommer | G-Moll | 315 | ||||
| Herbst | F-Dur | 293 | ||||
| Winter | F-Moll | 297 | ||||
| Flötenkonzert | D-Dur | Op. 10 ,Nr.3 | ||||
| „Il gardelino“ | ||||||
| Flötenkonzert | C-Dur | 443 | ||||
| Flötenkonzert | F-Dur | Op. 10, Nr. 5 | ||||
| C-Dur | 444 | |||||
| Flötenkonzert | C-Dur | |||||
| Flötenkonzert „La notte“ | G-Moll | Op. 10, Nr. 2 | 439 | |||
| Violinkonzert | Es Dur | Op. 8, Nr. 5 | ||||
| La tempesta die mare | ||||||
| CD-Li | Concerto per archi | |||||
| RV 159,153,121,129,154,115,143,141,120,156,158,123 | ||||||
| CD-Li | Concert für Streicher und Cembalo | |||||
| Symphonie | E-Moll | Op. 98, Nr. 4 | ||||
| Ungarische Tänze 1 und 2 | ||||||
| Mandolinen Konzert | C-Dur | RV425 | ||||
| Konzert für 2 Trompeten | C-Dur | RV 537 | ||||
| Konzert für Trompete und Violine | B-Dur | |||||
| Concerto Grosso | ||||||
| RV 562 a, 566, 569, 540, 561, 413, 553 | ||||||
| CD-Li | Konzert | F-Dur | Op. 10, Nr. 1 | RV 433 | ||
| CD-Ho | La temperata di mare | |||||
| Konzert | G-Moll | Op. 10, Nr. 2 | RV 439 | |||
| La notte | ||||||
| Konzert | D-Dur | Op. 10, Nr. 3 | RV 428 | |||
| Il gardelino | ||||||
| Konzert | F-Dur | Op.10, Nr. 5 | RV 434 | |||
| Konzert | G-Dur | Op. 10, Nr. 6 | RV 437 | |||
| Konzert | A-Moll | RV 440 | ||||
| CD-H | Fagott Konzerte | F-Dur | RV 485 | |||
| Fagott Konzerte | B-Dur | RV 503 | ||||
| Fagott Konzerte | Es-Dur | RV 483 | ||||
| Fagott Konzerte | A-Moll | RV 497 | ||||
| Fagott Konzerte | C-Dur | RV 473 | ||||
| Fagott Konzerte | G-Dur | RV 492 | ||||
| Violinkonzert | B-Moll | RV 386 | ||||
| Violinkonzert | D-Moll | RV 235 | ||||
| Violinkonzert | F-Dur | RV 296 | ||||
| Violinkonzert | E-Dur | RV 258 | ||||
| Violinkonzert | B-Moll | RV 389 | ||||
| Violinkonzert | E-Dur | RV 251 | ||||
| CD-H | Violinkonzert La caccia | D-Dur | Op. 8, Nr. 10 | |||
| Violinkonzert | D-Moll | RV 565 | ||||
| Violinkonzert | A-Dur | RV 552 | ||||
| Violinkonzert „Il piacere“ | C-Dur | Op. 8, Nr. 6 | ||||
| Violinkonzert “ per Pinsendel“ | D-Moll | Op. 8, Nr. 7 | ||||
| Streichkonzert | C-Dur | RV 113 | ||||
| Streichkonzert | C-Moll | RV 119 | ||||
| Streichkonzert | D-Dur | RV 121 | ||||
| Streichkonzert | D-Moll | RV 128 | ||||
| Streichkonzert | E-Moll | RV 133 | ||||
| Streichkonzert | F-Dur | RV 137 | ||||
| Streichkonzert | F-Dur | RV 141 | ||||
| Streichkonzert | G- Dur | RV 150 | ||||
| Streichkonzert | G-Moll | RV 154 | ||||
| Streichkonzert | G-Moll | RV 157 | ||||
| Streichkonzert | A-Dur | RV 160 | ||||
| Streichkonzert | B-Dur | RV 166 | ||||
| Trompetenkonzert | C-Dur | RV 537 | ||||
| Mandolinen Konzert | C-Dur | RV 425 | ||||
| Oboen Konzert | G-Moll | RV 460 | ||||
| Flötenkonzert | A-Dur | RV 585 | ||||
| Oboen Konzert | C-Dur | RV 447 | ||||
| Oboen Konzert | B -Dur | RV 479 | ||||
| Flötenkonzert | RV 162 | |||||
| 90 | Viviani, Giovanni | 1638-1692 | Buonaventura Sonata prima für Trompete und Orgel | C-Dur | Op. 4, Nr. 1 | |
| CD-Li | Sonate für Trompete | E-Moll | ||||
| 49 | Viacini, Giovanni Battista | Violinkonzert | A-Moll | Nr. 22 | ||
| 35 | Vincence, Frantisek | Serenade | C-Moll | |||
| 51 | Viotti, Giovanni Battista | 1755-1824 | Konzert für Flöte | A-Dur | ||
| 74 | Konzert für Violine und Orchester | A-Moll | Nr. 22 | |||
| weitere: Violinkonzert | E-Moll | Nr. 16 | ||||
| H-Moll | Nr. 24 | |||||
| 41 | Vanhall, Johann Batist | 1739-1813 | arbeitete mit v.Ditterdorf, Sinfonia | F-Dur | ||
| 103 | Sinfonia | G-Moll | ||||
| B 15 | Veracini | 1650-1733 | Streichorchester | |||
| 14, 43 | Wagenseil, Georg Christoph | 1715-1777 | Konzert für Harfe und Orchester | G-Dur | ||
| 32 | Konzert für Violine und Cello | A-Dur | ||||
| 44 | Posaunenkonzert | S-Dur | ||||
| 48 | Sinfonie | D-Dur | ||||
| CD-Li | Konzert flat | E-Dur | ||||
| 93 | Wassenahr, Graf von Unico Wilhelm | Konzert Violine Pergoresi | G-Dur | Nr. 2 | ||
| 68 | Konzert aus Concerto armonici | F-Moll | Nr. 4 | |||
| 96 | Konzert | S-Dur | Nr. 6 | |||
| 30 | Weiss, Silvius Leopold | 1686-1730 | Suite für Laute | F-Moll | Nr. 17 | |
| 43 | Zelenka, Jan Dismas | 1649-1745 | Capriccio 1 | D-Dur | ||
| 68 | Capriccio 2 | D-Dur | ||||
| 43 | Zimmermann, Anton | 1741-1781 | Sinfonie (war Joseph Heydn zugeschrieben) | C-Dur | ||
Literatur
Baumgartner, Alfred Alte Musik 1981 fünf Bände Kiesel Vgl. Salzburg
Bühler, Walther Das Pentagramm und der Goldene Schnitt als Schöpfungsprinzip
2001 Verlag Freies Geistesleben
Charpentier, Louis Das Geheimnis der Kathedrale von Chartres Knauer Taschenbuch
Caspar, Prof. Keppler Biographie
Denison, Isa Der göttliche Code Entstehung der Runen vor 250 000 Jahren. Vorbild ist das Eiskristall. Runen der EDDA, Govinda Vgl. Jestetten 2004
Eichler Richard W. Viel Gunst für schlechte . Kunst, Lehmanns Verlag 1968 . . . (Kunstförderung nach. 1945)
Eichler Richard W. Könner, Künstler, . . . .. Scharlatane, Verlag Amalthea, Wien 1978 . .. ..Was ist gute Kunst, und was ist gar eine Kunst?
Fölsing A. Galileo Galilei Prozess ohne Ende 1983 Piper Verlag
Fischer, Michael „Da berühren sich Himmel und Erde“ Musik und Spiritualität Benzinger Verlag Zürich, Düsseldorf 1998
Gorsleben, Rudolf John Hoch-Zeit der Menschheit Entstehen-Sein-Vergehen, Ursprache-schrift-glaube Koehler Verlag Leipzig 1923 Reproduktion: Burkhard Weeke Mittelstr.51 3285 Horn Bad Meinberg Tel. 05234-3780
Henning, Herbert, Wolfram Eid, Christian Hartfeldt Mathematik in der Welt der Töne
Technical Report Nr. 3/02, Fakultät für Mathematik, Universität Magdeburg, 2002.
Hesse, Hermann Das Glasperlenspiel, 1972 Suhrkamp Taschenbuch
Hofstadter, Douglas Übereinstimmungen der Ideen des Philosophen Gödel dem Maler Escher und dem Komponisten J.S. Bach Ein endloses geflochtenes Band. 844 Seiten 1986 Klett Cotta Vgl.
Lorenz, K. Das Wirkungsgefüge der Natur Piper Verlag München 1983
Mayer, Hans, Winklbauer, Günther Biostrahlen 1985 Woher sie kommen, was sie tun, wie sie wirken, Der Mensch im Strahlungsfeld von Kosmos, Erde und Umwelt. Orac Vgl. Wien
Missbach, Wochenbrief Vertrauliche Mitteilungen, Bücken
Mountbatten-Windsor, Charles Harmonie 2010, 320 Seiten. Eine neue Sicht unserer Welt.Riemann Vgl. München
Pinner, Reiß Über die bildende Kunst Wolfram Pinner J. Reiß, 86845 Großaitingen, Lindenweg 2, Pröll-Druck, Augsburg
Schintling-Horny, Volker von Der Bien im asymmetrischen Siebenstern 2003/2007 Kreisaufstellung der Bienenstöcke harmonisiert die Erde und verhindert Milbenbefall LSH Verlag Hülsenbergweg 110 40885 Ratingen. ISBN 978-3-00-021893-4
Schintling-Horny, Volker von Gute Gedanken aufgelesen 400 Seiten, Kunst, Politik, Familie, Naturkundliches, Benker, Weisheiten.Roman Verlag , 01587 Riesa
Schintling-Horny, Volker von Musik ist Leben 2014 LSH Verlag Ratingen
Stöhr, Manfred Der Mensch ist mehr als sein Gehirn Hirnforschung und Geistesfreiheit Verlag: Via Nova Petersberg 2012
Walter, Meinhard „Ein Hauch der Gottheit ist Musik“ Gedanken grosser Musiker Benzinger Verlag Zürich, Düsseldorf, 1999